Alt-F4 #47 – Lösungsoptimierung 17.09.2021

Geschrieben von ilbJanissary, editiert von stringweasel, Nanogamer7, Conor_, Therenas, Firerazer,
übersetzt von EDLEXUS, marceljoint, lektoriert von dexteritas

Inhaltsverzeichnis

Nach einer Dreiwöchigen Unterbrechung ist Alf-F4 wieder zurück, mehr motiviert denn je! Wir starten mit einem Paukenschlag, da ilbJanissary erklärt ausführlich, wie die Berechnungs-Engine hinter FactorioLab ihre Magie entfaltet. Auf den ersten Blick mag es kompliziert erscheinen, aber der Prozess ist in einzelne Teile untergliedert, die mit konkreten Beispielen illustriert werden. Bei der Lektüre dieses Artikels werden euch (hoffentlich!) nicht die Augen zufallen.

Lösungsoptimierung ilbJanissary

Hi! Als Angularentwickler und Langzeitnutzer von Kirk McDonald´s Factorio Rechner habe ich mich in 2020 dazu entschlossen, meinen eigenen webbasierten Rechner für Fabrikspiele, FactorioLab zu entwickeln. Kirk McDonald veröffentlichte einen Artikel über seinen Ansatz, der mir zu Beginn viel geholfen hat, allerdings hat er nicht den Algorithmus erklärt, mit dem die Lösung gefunden wird. Nach viel Kopfzerbrechen und zwei nicht-simplex Versionen von FactorioLab, will ich nun mit der Community teilen, was ich gelernt habe und wie ich einen echten Simplex-Algorithmus implementiert habe. Ein Zl;Ng findet ihr am Ende des Artikels.

Warum einen Rechner benutzen?

Fangen wir am Anfang an. Im Fabrikspielen wie Factorio, Dyson Sphere Program, und Satisfactory ist es das Ziel, Ressourcen abzubauen und diese Ressourcen mit Rezepten zu Gegenständen zu verarbeiten, um dann mit diesen Gegenständen fortgeschrittenere Gegenstände und Rezepte zu finden. Zu Beginn sind diese Rezepte einfach und noch übersichtlich, aber mit dem Spielfortschritt werden die Rezepte und Produktionsketten größer, unübersichtlicher und bedürfen mehr Planung. Factoriorechner wie FactorioLab und Kirk McDonald´s Factorio Rechner sind dazu gedacht, einfacher herauszufinden, wie viele Ressourcen und Fabrikgebäude für einen bestimmten Output benötigt werden.

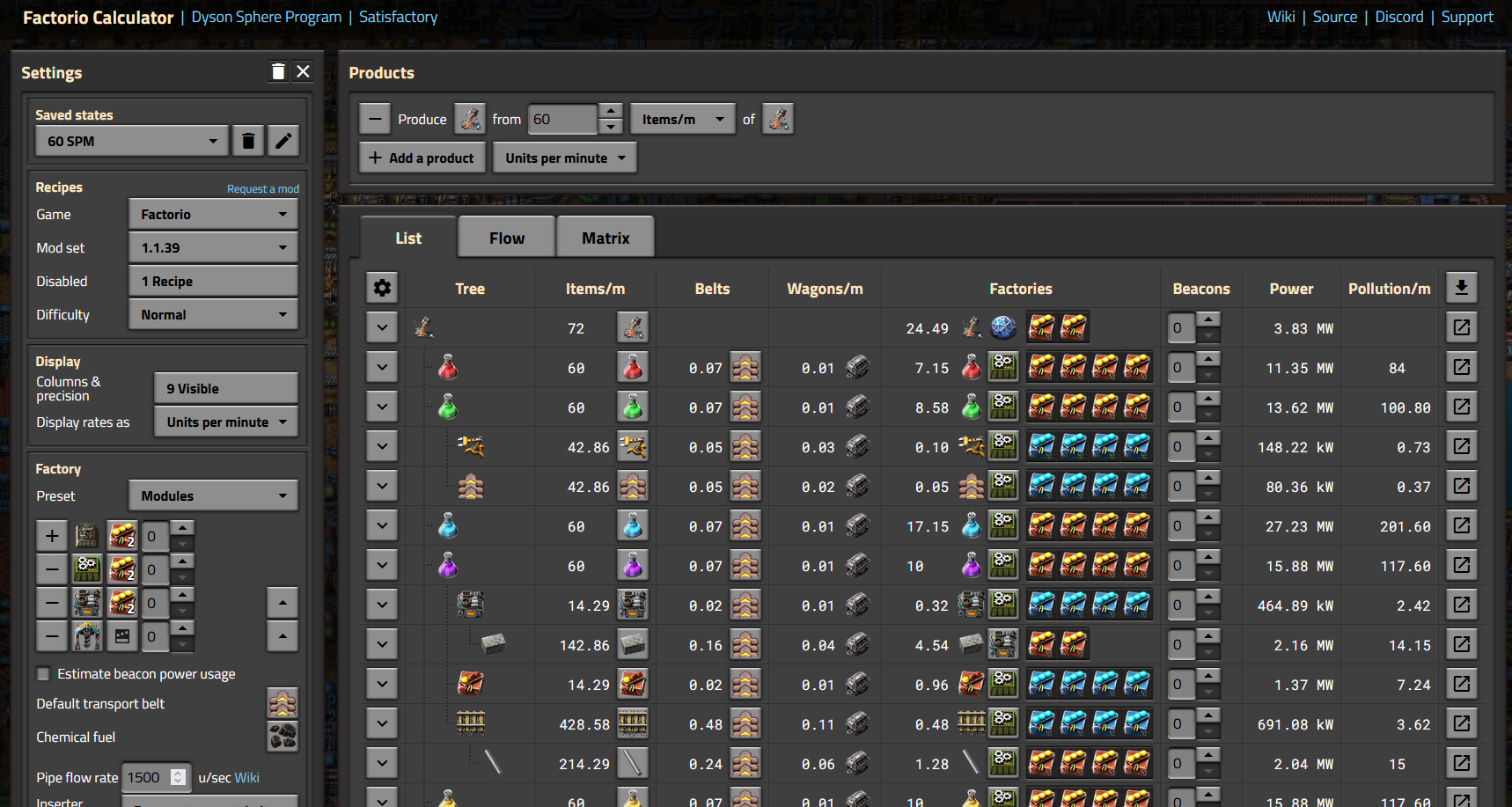
Konzepte

Es gibt zwei wichtige Konzepte in Fabrikspielen, die wichtig sind, um die Mathematik hinter den Berechnungen zu verstehen: Gegenstände und Rezepte.

Gegenstände sind die Produkte und Bestandteile in Fabrikspielen. Einige Gegenstände existieren nur als Zwischenprodukte und können selbst nichts tun, wie die meisten Ressourcen. Einige Gegenstände haben eine Bedeutung im Spiel, wie Treibstoff, Fließbänder, Öfen, Montagemaschinen, Generatoren, Strommästen und so weiter …
Rezepte sind die Methoden, wie der Spieler neue, fortgeschrittene Gegenstände im Spiel herstellt. Manche Gegenstände können per Hand hergestellt werden, andere können nur in speziellen Maschinen gefertigt werden. Rezepte benötigen in der Regel eine spezifische Anzahl an Ausgangsstoffen, bedürfen einer bestimmten Zeit und produzieren eine bestimmte Anzahl an Produkten. Rezepte werden oft als Liste an Ausgangsstoffen und der benötigten Zeit auf der linken Seite dargestellt mit einem Pfeil, der auf eine Liste an Produkten auf der rechten Seite zeigt.

Ein grundlegender Gegenstand in Factorio ist beispielsweise Eisenerz. Eisenerz ist ein Rohstoff, wird also in einem Rezept hergestellt, welches keines Eingangs bedarf:

Dieses Rezept kann auf Eisenerzvorkommen hergestellt werden, entweder per Hand oder mithilfe eines Erzförderers. Eisenerz wird hauptsächlich als Ausgangsstoff für Eisenplatten verwendet, welche ihr eigenes Rezept besitzen:

Eisenplatten können nicht per Hand hergestellt werden, sondern benötigen einen Ofen. Rezepte können auch viele Ein- und Ausgangsstoffe aufweisen, wie beispielsweise eins der komplexeren Rezepte in Factorio, Fortgeschrittene Ölverarbeitung:

Rezept der Fortgeschrittenen Ölverarbeitung

Dieses Rezept kann nur in einer Ölraffinerie hergestellt werden.

Herstellungsgeschwindigkeit

Die echte Herstellungszeit ist auch von der Geschwindigkeit der Maschine abhängig, die verwendet wird, um das Rezept herzustellen. Zum Beispiel besitzt der 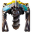Elektrische Erzförderer eine Herstellungsgeschwindigkeit von 0,5 und benötigt somit zwei Sekunden, um ein Eisenerz mit dem obigen Rezept herzustellen. Zur Vereinfachung gehen wir einfach allgemein von einer Herstellungsgeschwindigkeit von 1 aus.

Rezeptgleichungen

Es ist vielleicht aufgefallen, dass man, wenn man den Pfeil mit einem Gleichheitszeichen tauscht, das Rezept auch einfach als Gleichung auffassen kann. Da Zeit kein richtiger Gegenstand ist, müssen wir auf beiden Seiten mit der benötigten Zeit dividieren. Somit sind die Zahlen auf den jeweiligen Seiten der Gleichung nicht mehr feste Anzahlen, sondern Raten. Das Rezept für Eisenerz wird damit zu:

In diesem Fall ist die linke Seite der Gleichung Null, da das Rezept keines Eingangs bedarf. Analog dazu wird das Rezept für Eisenplatten zu:

Bis zu einem gewissen Punkt sind diese Gleichungen relativ simpel zu lösen. Viele Gegenstände können nur von einem einzigen Rezept hergestellt werden und benötigen daher nur einfache Algebra, um die Anzahl der Gegenstände und Rezepte herauszufinden, die für eine bestimmte Produktionsrate gebraucht werden. In FactorioLab werden, wenn der Gegenstand nur durch ein Rezept hergestellt werden kann, die Gleichungen direkt so weit wie möglich gelöst. Ist es aber möglich, einen Gegenstand mit verschiedenen Rezepten herzustellen, wird es viel schwieriger herauszufinden, welches Rezept, oder meistens, welche Mischung aus Rezepten nötig sind, um die gewünschte Menge mit möglichst wenigen Ressourcen herzustellen.

Rezeptmatrizen

Das typische Problem in Factorio ist Fortgeschrittene Ölverarbeitung und Cracken, und es wird im Folgenden verwendet, um darzustellen, wie eine Lösung gefunden wird. Dieses Problem umfasst in der Regel mindestens fünf Rezepte und fünf Gegenstände. Die Rezepte sind:

Rohöl (Rohstoff)

Die Rohölproduktionsgeschwindigkeit variiert je nach der Ressource auf der Karte, wird aber hier vereinfacht behandelt.

Wasser (Rohstoff)

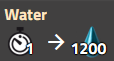
Fortgeschrittene Ölverarbeitung

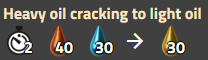
Schwerölcracken

Leichtölcracken

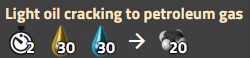
Es werden unter Umständen auch andere Rezepte verwenden, wie Grundlegende Ölverarbeitung oder Kohleverflüssigung, welche aber hier ignoriert werden.

Durch Division mit den jeweils benötigten Zeiten ergibt sich jetzt eine Gleichung mit Raten, welche die Form hat, die der Rechner benötigt, um die Produktionsanforderungen zu berechnen. Da die Herstellungsgeschwindigkeit aller beteiligten Fabriken 1 ist, müssen wir an dieser Stelle keine besonderen Anpassungen machen. Diese wären aber nötig, falls mehr Fabriken mit verschiedenen Geschwindigkeiten oder Effektverteilern beteiligt wären.

Rohöl (Rohstoff)

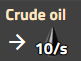
Wasser (Rohstoff)

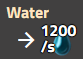
Fortgeschrittene Ölverarbeitung

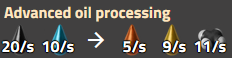
Rate der fortgeschrittenen Ölverarbeitung

Schwerölcracking

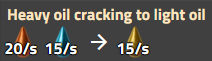
Leichtölcracken

Diese Rezepte können in einer Matrix angeordnet werden. Die Matrix hat verschiedene Spalten für Rezepte und Zeilen für Gegenstände. Das schafft eine andere Gruppe Gleichungen, jeweils eine Gleichung pro Gegenstand. Beispielsweise für Rohöl: 10 - 20 = # Ertrag

Nach dem Teilen der Anzahl durch ihre jeweils benötigte Zeit sieht die vollständige Matrix folgendermaßen aus:


10	0	-20	0	0
0	1200	-10	-15	-15
0	0	5	-20	0
0	0	9	15	-15
0	0	11	0	10

Als Nächstes müssen wir uns darum kümmern, was unsere Fabrik herstellen soll. Dafür können wir eine weitere Spalte verwenden, welche das Endergebnis unserer Fabrik darstellt. Sagen wir beispielsweise, wir wollen 5 Schweröl/Sekunde und 100 Petroleum/Sekunde herstellen. Um das in der Matrix darzustellen, müssen die Werte negativ sein, da wir zeigen, dass wir diese Produkte aus dem System entnehmen.

					Ausgang
10	0	-20	0	0	0
0	1200	-10	-15	-15	0
0	0	5	-20	0	-5
0	0	9	15	-15	0
0	0	11	0	10	-100

Lineare Optimierung

Eine Matrix dieser Art nennt sich in der Mathematik lineare Optimierung und kann mit linearen Optimierungstechniken gelöst werden. Die am weitesten verbreitete Art, solche Probleme zu lösen, ist das Simplex-Verfahren. Diese Methode wird sowohl von FactorioLab, als auch von Kirk McDonald´s Factorio Rechner verwendet. Da es mehrere mögliche Lösungen für diese Matrix gibt, versucht das Simplex-Verfahren den Wert einer Objektfunktion zu maximieren, welche im Prinzip eine andere Spalte Zeile in der Matrix darstellt.

Obwohl wir nicht wirklich etwas haben, was wir maximieren wollen, haben wir doch etwas, was wir minimieren wollen, nämlich die Anzahl der Fabriken und Rohstoffe. Anstelle eines Zielwert, welchen wir maximieren wollen, können wir eine Kostenfunktion hinzufügen, mit der wir beschreiben, wie wir die Anzahl an Rohstoffen minimieren wollen.

Warum brauchen wir eine Kostenfunktion?

Für einfache Fabriken, in denen es nur ein einzelnes Rezept pro Fabrik gibt, benötigen wir gar keine Kostenfunktion. Wir können berechnen, wie viel von jedem Bestandteil wir benötigen, und können uns so Schritt für Schritt vorarbeiten, bis wir eine Lösung erhalten. Warum braucht nun also unsere lineare Optimierung eine Kostenfunktion?

Schauen wir uns unser Ölverarbeitungsbeispiel an. In unserem Beispiel wollen wir Flüssiggas und Schweröl herstellen. Beachte, das fortgeschrittene Ölverarbeitung beide Produkte herstellt. Deswegen ist eine mögliche Lösung, die Crackingrezepte einfach zu ignorieren und einfach alle Produkte direkt durch fortgeschrittene Ölverarbeitung herzustellen. Warum verwenden wir dann überhaupt Cracken in Factorio? Dafür gibt es zwei Gründe:

Die Gleichung ist nicht ausgeglichen, das Produktverhältnis wird sich also nicht mit dem geforderten Verhältnis decken, und so wird es zu einem Rückstau kommen, der die gesamte Produktion aufhalten wird. In den meisten Fabriken, welche nur Wissenschaftspakete herstellen, ist der Übeltäter meist Leichtöl. Es gibt keine Möglichkeit, Überproduktionen in Factorio einfach abzufackeln, und das manuelle Leeren der Tanks ist anstrengend.
Es verwendet übermäßig viel Rohöl. Rohöl ist nicht so einfach zu beschaffen wie Wasser, weswegen wir in der Regel den Bedarf minimieren wollen. Durch das cracken von Leichtöl in Petroleum können wir uns sowohl um das Leichtöl kümmern und gleichzeitig die Menge an Rohöl verringern und benötigen dafür nur mehr Wasser, welches leichter zu beschaffen ist.

Eine Kostenfunktion quantifiziert, wie schwer es ist, eine bestimmte Ressource zu beschaffen und wie groß der Aufwand ist, um die benötigten Fabriken zu bauen. Eine Lösung, welche weniger Ressourcen benötigt ist besser als eine Lösung, welche mehr Ressourcen bedarf, und eine Lösung, die wenige Fabriken benötigt, ist besser als eine Lösung, welche viele Fabriken benötigt. Durch das zuweisen spezieller Werte für die Beschaffung spezifischer Ressourcen und Fabriken können wir die Kosten einer Lösung direkt quantifizieren, und der Rechner kann angewandt werden, um herauszufinden, welche Lösung optimal ist.

Wie definieren wir eine Kostenfunktion?

Die Kostenfunktion kann relativ abstrakt und zufällig gewählt sein, da Rohstoffe und Fabriken keine spezifischen Kosten in Fabrikspielen wie Factorio oder Dyson Sphere Program haben. Stattdessen vertrauen wir auf unsere Intuition, welche Ressourcen schwerer oder aufwendiger zu fördern sind. In FactorioLab kommt es dadurch auf einige spezifische Faktoren, welche die Kostenfunktion definieren:

Eine einzelne Fabrik, welche ein Rezept abarbeitet, kostet 1.
Eine Einheit Wasser kostet 100, da Wasser einfach zu beschaffen ist.
Eine Einheit Rohöl kostet 1000, da es üblicherweise in größeren Mengen gefördert wird als andere Bodenschätze.
Eine Einheit Bodenschätze kostet 10,000. In Factorio gilt dies für Kohle, Uranerz, Stein, Eisenerz, und Kupfererz. Dies sind die Ressourcen, deren Verbrauch wir generell minimieren wollen.
Eine Einheit händisch abgebauter Ressourcen kostet 100,000. In Factorio gilt dies beispielsweise für Holz. Während Holz nicht wirklich eine Rolle in Factoriorezepten spielt, wollen wir den Bedarf aller Materialien, die nicht automatisch gefördert werden können, minimieren.

Wir können diese Kostenfunktion als zusätzliche Zeile in unserer Matrix darstellen. Um akkurat die Kosten der benötigten Ressourcen berechnen zu können, vereinfachen wir die Rezepte so, dass die Kosten auf der Menge der benötigten Gegenstände basieren und nicht auf der Anzahl der Gebäude, die diesen Rohstoff fördern. Deshalb sind die Förderpumpe und Gewässerpumpe -Rezepte vereinfacht zu teureren Rezepten, die nur eine Einheit pro Sekunde herstellen. Nachdem wir die benötigte Menge Rohöl und Wasser herausgefunden haben, ist es trivial, diese Werte in Fabrikanzahlen umzusetzen.

						Ausgang
	1	0	-20	0	0	0
	0	1	-10	-15	-15	0
	0	0	5	-20	0	-5
	0	0	9	15	-15	0
	0	0	11	0	10	-100
Kosten	1000	100	1	1	1	0

Doppelminimierungsproblem

Jetzt ist das Problem unserer linearen Optimierung, das wir einen Wert minimieren wollen, während das Simplex-Verfahren einen Wert maximieren möchte. Glücklicherweise gibt es einen einfachen Weg, ein Minimalproblem in ein Maximalproblem zu überführen, welches dann mit dem Simplex-Verfahren gelöst werden kann. Dies wird ermöglicht durch die Konvertierung in ein Doppelmaxmierungsproblem. Wenn das Problem in die Doppelmaximierungsform übertragen ist, kann das Problem mit dem Simplex-Verfahren gelöst werden. Die Lösung für das Maximalproblem ist dieselbe wie für das Minimalproblem, sodass wir diese Lösung akzeptieren können.

Das Doppelproblem ist einfach die transformierte Form des Originalproblems, so das wir nur Zeilen und Spalten vertauschen müssen:

						Kosten
	1	0	0	0	0	1000
	0	1	0	0	0	100
	-20	-10	5	9	11	1
	0	-15	-20	15	0	1
	0	-15	0	-15	10	1
Ausgang	0	0	-5	0	-100	0

Um mögliche Nebenprodukte abzudecken, werden in der linearen Optimierung Nebenprodukte mitaddiert. Eine Fabrik, welche beispielsweise nur Schweröl herstellt, produziert gezwungenermaßen auch Leichtöl und Flüssiggas. Diese Nebenprodukte werden durch zusätzliche Spalten in der Matrix angezeigt, wobei jede Spalte eine “1” in der entsprechenden Produktzeile besitzt.

						+	+	+	+		Kosten
	1	0	0	0	0	1	0	0	0	0	1000
	0	1	0	0	0	0	1	0	0	0	100
	-20	-10	5	9	11	0	0	1	0	0	1
	0	-15	-20	15	0	0	0	0	1	0	1
	0	-15	0	-15	10	0	0	0	0	1	1
Ausgang	0	0	-5	0	-100	0	0	0	0	0	0

Jetzt haben wir endlich eine Matrix, welche wir mit dem Simplex-Verfahren lösen können.

Lösung mit Simplex

Das Ziel des Simplex-Verfahrens ist es, die Matrix so umzuformen, das die Zielfunktion (in diesem Fall die letzte Zeile der Matrix) keine negativen Zahlen mehr enthält. In unserer Initialmatrix besitzt unsere Zielzeile zwei negative Spaltenwerte, welche die zwei Gegenstände darstellen, die wir herstellen wollen. Um unsere Lösung zu erreichen, müssen wir Pivotoperationen anwenden, bis unsere Objektzeile keine negativen Werte mehr enthält.

Pivot 1

Eine Simplex Pivotoperation besteht aus vier Schritten.

Wähle eine Spalte. Das muss eine Spalte mit negativen Wert sein, in der Regel wählt man den größten aus. In unserer Matrix wäre das die Flüssiggasspalte.
Wähle eine Reihe. Überprüfe jede Zeile, in der die gewählte Spalte einen positiven Wert besitzt, und berechne das Verhältnis der Kostenspalte in dieser Reihe zum Wert der gewählten Spalte in dieser Reihe. Die Pivotzeile ist die Zeile mit dem geringsten Verhältnis. In unserer Matrix können wir jede Zeile überprüfen:
1. : Spalte ist 0, also ignorieren wir die Zeile.
2. : Spalte ist 0, also ignorieren wir die Zeile.
3. : Spalte ist 11, die Kosten sind 1, das Verhältnis ist also 1/11.
4. : Spalte ist 0, also ignorieren wir die Zeile.
5. : Spalte ist 10, die Kosten sind 1, das Verhältnis ist also 1/10.
6. Das geringste Verhältnis hat die Reihe bei 1/11, also wählen wir diese aus.
Dividiere die Pivotzeile mit durch den Kehrwert des Pivotelements. In unserem Fall führt dies zu -20/11, -10/11, 5/11, 9/11, 1, 0, 0, 1/11, 0, 0, 1/11
Addiere das Vielfache der Pivotzeile zu den anderen Zeilen, um in die Pivotspalte zu 0 zu ändern. Das Ergebnis ist:

+	+	+	+	+						Kosten
1	0	0	0	0	1	0	0	0	0	1000
0	1	0	0	0	0	1	0	0	0	100
-1 9/11	-10/11	5/11	9/11	1	0	0	1/11	0	0	1/11
0	-15	-20	15	0	0	0	0	1	0	1
18 2/11	-5 10/11	-4 6/11	-23 2/11	0	0	0	-10/11	0	1	1/11
-181 + 9/11	-90 10/11	40 5/11	81 9/11	0	0	0	9 1/11	0	0	9 1/11

Jetzt fahren wir mit dem nächsten Pivot fort.

Pivot 2

Spalte 1 (-181 9/11), Zeile 5 (Verhältnis 1/200)

+	+	+	+	+						Kosten
0	13/40	1/4	1 + 11/40	0	1	0	1/20	0	-11/200	9999 + 199/200
0	1	0	0	0	0	1	0	0	0	100
0	-1 1/2	0	-1 1/2	1	0	0	0	0	1/10	1/10
0	-15	-20	15	0	0	0	0	1	0	1
1	-13/40	-1/4	-1 11/40	0	0	0	-1/20	0	11/200	1/200
0	-150	-5	-150	0	0	0	0	0	10	10

Pivot 3

Spalte 2 (-150), Zeile 2 (Verhältnis 100)

+	+	+	+	+						Kosten
0	0	1/4	1 + 11/40	0	1	-13/40	1/20	0	-11/200	9967 + 99/200
0	1	0	0	0	0	1	0	0	0	100
0	0	0	-1 1/2	1	0	1 1/2	0	0	1/10	150 + 1/10
0	0	-20	15	0	0	15	0	1	0	1501
1	0	-1/4	-1 11/40	0	0	13/40	-1/20	0	11/200	32 + 101/200
0	0	-5	-150	0	0	150	0	0	10	15010

Pivot 4

Spalte 4 (-150), Zeile 4 (Verhältnis 133 2/5)

+	+	+	+	+						Kosten
0	0	1 19/20	0	0	1	-1 3/5	1/20	-17/200	-11/200	9839 + 91/100
0	1	0	0	0	0	1	0	0	0	100
0	0	-2	0	1	0	3	0	1/10	1/10	300 + 1/5
0	0	-1 1/3	1	0	0	1	0	1/15	0	100 + 1/15
1	0	-1 19/20	0	0	0	1 3/5	-1/20	17/200	11/200	160 + 9/100
0	0	-205	0	0	0	300	0	10	10	30020

Pivot 5

Spalte 3 (-205), Zeile 1 (Verhältnis 5046 7/65)

+	+	+	+	+						Kosten
0	0	1	0	0	20/39	-32/39	1/39	-17/390	-11/390	5046 + 7/65
0	1	0	0	0	0	1	0	0	0	100
0	0	0	0	1	1 1/39	1 14/39	2/39	1/78	17/390	10392 + 27/65
0	0	0	1	0	80/117	-11/117	4/117	1/117	-22/585	6828 + 41/195
1	0	0	0	0	1	0	0	0	0	1000
0	0	0	0	0	105 5/39	131 31/39	5 10/39	1 5/78	4 17/78	1064472 + 1/13

Die letzte Zeile der Matrix besitzt nun keine negativen Werte, die Matrix ist also eine gültige Lösung. Die Lösung kann nun aus der letzten Zeile extrahiert werden, in der die ersten fünf Werte die Nebenprodukte darstellen (in diesem Fall alle Null), die nächsten zwei Werte die Eingangsmaterialien Rohöl und Wasser, die nächsten drei Werte die Anzahl der Fabriken, welche Fortgeschrittene Ölverarbeitung, Schwerölcracken, und Leichtölcracken durchführen, und der letzte Wert beschreib die Kosten dieser Lösung.

Unsere Lösung benötigt 105 5/39 , 131 31/39 , 5 10/39 , 1 5/78 , and 4 17/78 .

Diese Lösung kann verglichen werden mit dem Ergebnis in FactorioLab.

Matrixtab

Der Matrix Tab in FactorioLab, ein relativ neues Feature, ermöglicht es dir, einmal hinter die Kulissen zu schauen. Für jede Produktionskette, die auch ohne Simplex gelöst werden kann, ist dieser Tab relativ leer, aber wenn Simplex verwendet wird, zeigt dieser Tab viele Details und ermöglicht es sogar, die Kostenfunktion individuell anzupassen.

Ergebnisinformationen

Die erste Tabelle zeigt Details der aktuellen Simplexlösung.

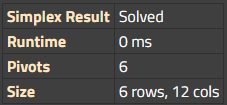
Die Simplex Lösung des Rechners
- Skipped: Der Simplexlöser wurde nicht verwendet, entweder weil er nicht nötig war oder deaktiviert ist.
- Failed: Der Simplexlöser hat einen Fehler gefunden, in der Regel durch eine zyklische Abhängigkeit, die nicht gelöst werden kann (beispielsweise wenn Eisenplatte zwei Eisenzahnräder benötigen und Eisenzahnräder zwei Eisenplatten)
- Cancelled: Der Benutzer hat den Simplexlöser manuell nach mindestens fünf Sekunden Rechenzeit abgebrochen.
- Solved: Eine gültige Lösung wurde gefunden.
Die Runtime des Simplexlösers in ms
Die Gesamtanzahl an durchgeführten Pivots
Die Size der Matrix

Kostenmodifikatoren

Die zweite Tabelle erlaubt es dem Nutzer, die Kostenfunktion anzupassen.

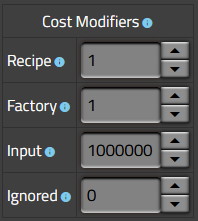
Recipe ist ein Faktor, der Rezeptkosten mit definierten Kosten multipliziert, in der Regel Abbaurezepteingänge
Factory ist ein Faktor, der die Kosten der Fabriken multipliziert; oft nicht Hauptziel
Input definiert die Kosten von Gegenständen, die nicht per Rezept hergestellt werden können, wie Holz
Ignored definiert die Kosten von Gegenständen, welche ignoriert werden sollen, standartmäßig Null

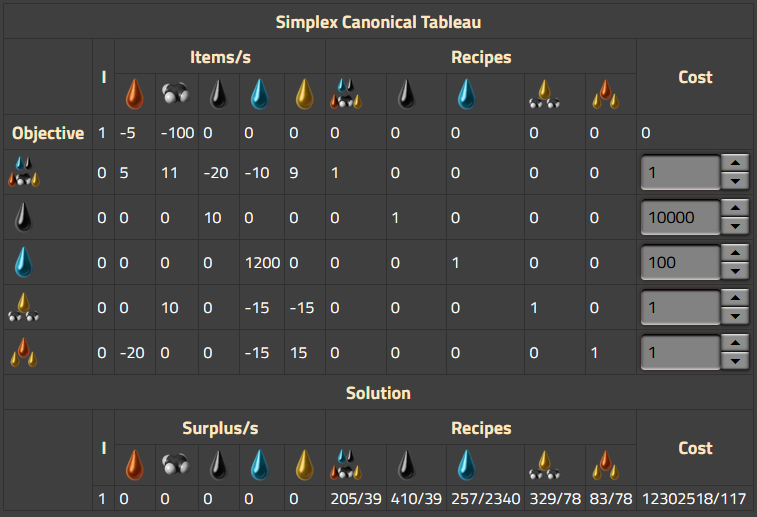
Simplex kanonische Form und Ergebnis

Die dritte Tabelle zeigt sowohl die von dem Rechner generierte kanonische Matrix als auch die Ergebniszeile mit den finalen Kosten. Beachtet, dass dies als Doppelminimierungsproblem dargestellt wird, so wie der Rechner die Kosten mittel Simplex-Methode minimiert. In jeder Zeile werden die Kosten des Rezeptes angezeigt und können auch mithilfe des Kosteneingabefeldes auf der rechten Seite überschreiben werden. Die Werte werden unabhängig von der vom Nutzer gewählten Anzeigerate in Gegenstände/Sekunde dargestellt, da die Berechnung intern immer auf diese Weise erfolgt.

Alternative Algorithmen

Der Simplex-Algorithmus mit Doppelmaximierung hat sich als sehr effektive Methode zur Lösung von Fabrikberechnungen erwiesen. Er ist allerdings nicht der einzige Algorithmus zur Lösung linearer Optimierungen. Es gibt noch andere Methoden wie das revidierte Simplex-Verfahren, Criss-Cross-Verfahren, Ellipsoidmethode, Karmarkar Algorithmus und das Innere-Punkt-Verfahren. Tatsächlich wurde erst 2019 die Laufzeit durch einen neuen Algorithmus zur Matrixmultiplikation verbessert. Da lineare Optimierungen groß werden können, insbesondere im modifiziertem Factorio, kann der von FactorioLab verwendete Simplex-Algorithmus sehr lange brauchen, um eine Lösung zu finde. Dies ist vor allem bei Mods der Fall, die “Recycling”-Rezepte einführen, die für eine große Anzahl an Schleifen sorgen. Mit weiterer Forschung ist es möglich, dass ein bessere Algorithmus zur Lösung von Fabrikprogrammen gefunden wird.

ZL;NG

Einfache Fabriken sind leicht von Hand zu berechnen, wenn Gegenstände nur nach einem einzigen Rezept hergestellt werden.
Wenn Gegenstände von mehreren verschiedenen Rezepten hergestellt werden, müssen wir einen Weg finden, um herauszufinden, wie viel von jedem Rezept verwendet werden soll.
Da es mehrere mögliche Lösungen gibt, müssen wir die Kosten einer Lösung messen, um die beste Lösung zu ermitteln.
Simplex ist der am häufigsten verwendete Algorithmus (wenn auch nicht der schnellste), um diese Art von Problemen zu lösen, sowohl in Factorio als auch in der Mathematikgemeinschaft.
FactorioLab verwendet den Simplex Algorithmus, um die Lösung für komplexe Fabriken zu optimieren und ermöglicht es den Nutzer:
- Anpassen der Kostenfunktion, da sie subjektiv ist
- Verbreitete Mods zu verwenden
- Berechnen und Planen der Fabrik vom mobilen Endgerät oder Arbeitsplatz aus
- Zu berechnen, wie viel Raketenbrennstoff eine einzelne Raffinerie produzieren könnte

Tritt dem FactorioLab Discord bei, um mehr zu erfahren!

Beitragen

Wie immer suchen wir nach Leuten, die zu Alt-F4 beitragen wollen, sei es mit einem Artikel oder durch Hilfe bei Übersetzungen. Wenn du etwas Interessantes im Kopf hast, das du mit der Community in einer eleganten Art teilen möchtest, hier kannst du das tun. Falls du dir unsicher bist, beantworten wir gerne Fragen zu Inhalt und Struktur. Falls das nach etwas klingt, woran du interessiert bist, tritt unserem Discord bei, um es nicht zu verpassen!

Im Factorio-Forum diskutieren Auf Reddit diskutieren Auf Discord diskutieren