Alt-F4 #11 - Curiosidades científicas 30-10-2020
traducido por G00S3MEISTER

Tabla de contenidos
-
Examen científico del mundo de Factorio
pocarski - Nauvis es una enana blanca
- Un poco sobre la mecánica orbital de Nauvis
- Nauvis refleja por lo menos el 88.3% de la luz que le llega
- Las armas nucleares tienen muy poca potencia
- El combustible nuclear es tres veces más caliente que la superficie del Sol
- Los objetos tienen densidades increíblemente bajas
-
Archivos de Nauvis: Técnicas obsoletas
stringweasel - Contribuir
Bienvenidos a la undécima edición de Alt-F4, os traemos un análisis matemático y una lección de historia. ¡Así que escucha, estudiante! Pocarski se encargó de ver si las matemáticas del mundo real funcionan en Nauvis. Alerta de spoiler: no es así. Luego, Stringweasel regresa una vez más para echar un vistazo a un poco de historia, esta vez enfocándose en mecánicas pasadas que ahora están obsoletas.
Examen científico del mundo de Factorio pocarski
La suspensión de la incredulidad es un concepto bien conocido, que no impide que algunos de nosotros lo ignoremos por completo. Recientemente vi un post de Reddit sobre calcular la densidad de Nauvis, y eso me dio la idea de hacer una compilación por pasar el rato de toda la ciencia ridícula que ocurre en el universo de Factorio. Después de todo, esta comunidad siempre ha sido un grupo de frikis con demasiado tiempo libre, así que ¿por qué no disfrutar de un poco de frikismo recreativo?
Advertencia obvia: este artículo contiene una cantidad excesiva de matemática; Si tiene una alergia grave a las matemáticas, no dude en omitirla.
Nauvis es una enana blanca
Este es una reedición de la publicación de Reddit de u/DaveMcW que acabo de mencionar. Tener en cuenta que esta teoría asume que el ciclo día / noche de Nauvis en realidad es causado por la rotación, que es algo sobre lo que discutiré más adelante.
Los grandes cuerpos celestes se mantienen unidos por la gravedad y, para que un planeta no se rompa por la fuerza centrífuga, la gravedad en el ecuador debe ser mayor que la fuerza centrípeta. Suponiendo un planeta esférico, y usando las ecuaciones para la fuerza centrípeta y la gravedad, podemos demostrar que:
$ \frac{GMm}{r^2} > mr\omega^2 $, donde $G$ es la constante de gravitación universal, $r$ el radio del planeta, $M$ la masa del planeta, $\omega$ la velocidad angular del planeta, y $m$ la masa del cuerpo sobre el que actúa el planeta;
$ \frac{GM}{r^2} > r\omega^2 \quad\Rightarrow\quad GM > r^3\omega^2 $
$ \frac{4}{3}\pi r^3 = V \quad\Rightarrow\quad r^3 = \frac{3V}{4\pi} $, donde $V$ es el volumen del planeta;
$ GM > \frac{3V\omega^2}{4\pi} \quad\Rightarrow\quad G\frac{M}{V} > \frac{3\omega^2}{4\pi} $
$ \omega = \frac{2\pi}{T} \quad\Rightarrow\quad \frac{3\omega^2}{4\pi} = \frac{3\pi}{T^2};\quad \frac{M}{V} = \rho $, donde $ \rho $ es la densidad del planeta;
$ \frac{G\rho}{3} > \frac{\pi}{T^2} \quad\Rightarrow\quad \rho > \frac{3\pi}{GT^2} $
Terminamos con una expresión de densidad dependiendo del período de rotación. Sustituyendo los valores de $ \pi $ y $G$, a través del periodo del ciclo día/noche (T = 25 000 ticks = 416,(6) seconds) obtenemos:
$ \rho > 813,400 \mathrm{kg/m^3} $
La densidad de Nauvis tiene que ser mayor que 813,400 kg/m3. Para comparar, la densidad del acero es de 8,050 kg/m3, la del plomo es de 11,350 kg/m3, y la del osmio, la sustancia más densa de la Tierra, 22,570 kg/m3. 813,400 kg/m3 es un número tan extremo que Nauvis debe ser una estrella enana blanca para ser tan densa. Una enana blanca es lo que queda después de que una pequeña estrella muere y sufre un colapso, dejando un remanente sobrecalentado del tamaño de la Tierra. Las enanas blancas tienen temperaturas superficiales de 8.000 K a 40.000 K. En comparación, la superficie del Sol está un poco por debajo de los 6.000 K. ¡El suelo Nauvis debe ser un aislante térmico excepcional!
Un poco sobre la mecánica orbital de Nauvis
Dado que todas las sombras permanecen en una longitud y dirección constantes durante todo el día, debemos concluir que la posición de la fuente de luz en el cielo no cambia, lo que significa que Nauvis tiene acoplamiento de mareas con su estrella. De ello se deduce que el ciclo día/noche que observamos es causado por algún objeto que ocluye la luz. Según la frecuencia de las noches, ese objeto probablemente esté en órbita alrededor de Nauvis, y no puede ser una luna, ya que una luna lo suficientemente grande para noches tan largas tendría también acoplamiento de mareas con Nauvis. Entonces, La noche debe ser causada por una nube de escombros en la órbita de Nauvis, lo que también proporciona una razón por la que el Ingeniero se estrellara allí, la nave chocó contra una roca en órbita.
Una explicación alternativa para el ciclo día/noche, propuesta por algunos, es que la estrella madre de Nauvis es una variable Cefeida, que es un tipo de estrella que varía en tamaño, temperatura y brillo en un patrón regular. Personalmente creo que esto es imposible ya que la variación de luminosidad es demasiado alta, especialmente en un período tan corto.
Nauvis refleja por lo menos el 88.3% de la luz que le llega
Un panel solar de Factorio tiene una área 9 m2 y produce 60 kW durante el día. De estos números, encontramos que la superficie recibe por lo menos 6.(6) kW/m2 (comparado con 1 kW/m2 de la Tierra). Considerando que la temperatura ambiente de Nauvis es de 15 °C, y que tiene acoplamiento de marea, podemos usar una fórmula de la temperatura efectiva ligeramente modificada:
$ T = \root{4}\of{\frac{1}{2}\frac{P(1-a)}{\sigma}} $, donde $P$ es la potencia recibida por unidad de área, $T$ la temperatura absoluta de la superficie, $a$ es el albedo (que es lo que tratamos de encontrar), y $\sigma$ es la constante de Stefan-Boltzmann;
$ a = 1 - \frac{2\sigma T^4}{P} $
$ T = 15\mathrm{°C} = 288,15\mathrm{K} $
$ P = 6666,(6)\mathrm{W/m^2} $
$ a = 0,8827 $
Nauvis debe tener un albedo de al menos 0,883 para mantener los 15°C. Esto significa que refleja al menos el 88.3% de la luz que le llega. Dado que la eficiencia de nuestros paneles solares es probablemente inferior al 100%, y Nauvis probablemente no sea un cuerpo negro ideal, es probable que el albedo sea aún mayor.
Como comparación, la Luna tiene un albedo de 0,14 y la Tierra tiene un albedo de 0,306. Si la Luna tuviera un albedo de 0,883, sería 6,3 veces más brillante. Si la Tierra tuviera un albedo de 0,883, tendría una temperatura superficial media de -88,5 ° C.
Las armas nucleares tienen muy poca potencia
Ahora es el momento de regresar del espacio y echar un vistazo a las cosas artificiales. Una pieza de Uranio-235 en Factorio puede producir 10 pilas de combustible, cada una de las cuales contiene 8 GJ (ignoremos la bonificación de vecino). Esto significa que una sola pieza de U-235 tiene 80 GJ de energía de fisión, y dado que una bomba nuclear usa 30 piezas de U-235, con una tasa de fisión del 20% (que es lo que obtienes con fisión intensificada; algo que se requiere para una bomba nuclear tan pequeña), debería tener un rendimiento explosivo de 115 toneladas de TNT. Eso no parece mucho, pero solo el sprite de explosión en sí mismo tendría 60 mosaicos de ancho. Tal arma nuclear destruiría todo completamente en un radio de 100 mosaicos, mataría todo en un radio de 250 mosaicos y haría daño en un radio de 500 mosaicos (basado en Nukemap).
A modo de comparación, la bomba nuclear en el juego solo hace daño dentro de un radio de menos de 40 casillas, por lo que esa es una diferencia de 12.5x en el área de efecto.
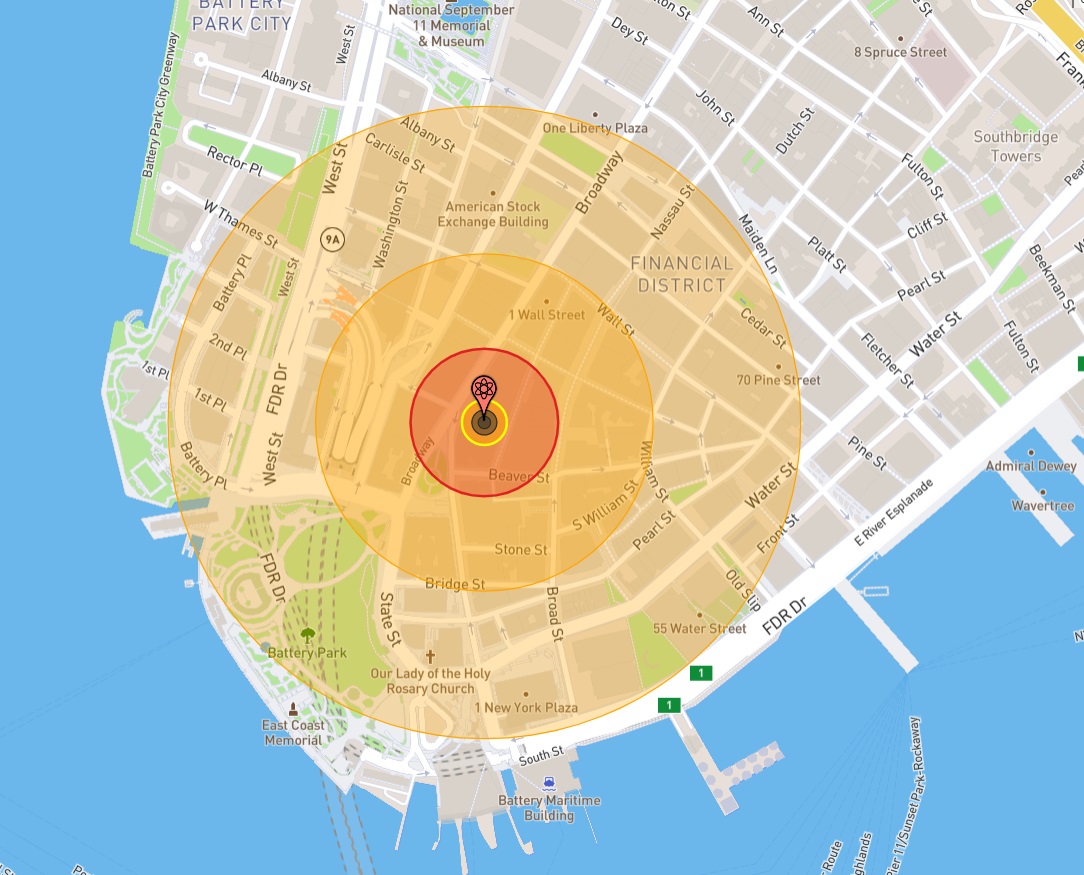
Los anillos del diagrama denotan, de más pequeño a más grande:
- Cráter y labio del cráter (sprite de la marca de quemadura)
- Bola de fuego (sprite de explosión)
- Gran daño a la estructura (la zona de “destrucción total”)
- 100% de probabilidad de quemaduras de tercer grado (la zona de “muerte total”)
- 50% de probabilidad de quemaduras de primer grado (la zona de “daño”)
Para ser completamente honesto, si consideramos que el U-238 también contribuye a la producción total de energía de una celda de combustible, obtenemos una bomba nuclear algo más pequeña. Sigue siendo ridículo, pero un poco menos.
Hablando de energía nuclear …
El combustible nuclear es tres veces más caliente que la superficie del Sol
Las locomotoras tienen un consumo de energía constante de 600 kW, pero un mejor combustible las hace más rápidas. Esto significa que el combustible de nivel superior aumenta la eficiencia del motor.
Podemos expresar la potencia generada a través de la aceleración y la velocidad:
$ P_u = \frac{dA}{dt} = \frac{Fds}{dt} = Fv = mav $, donde $P_u$ es la potencia útil, $m$ la masa del tren, $a$ la aceleración del tren, y $v$ la velocidad máxima del tren.
La eficiencia $N$:
$ N = \frac{P_u}{P_c} = \frac{mav}{P_c} $, donde $P_c$ la potencia total consumida (600 kW);
$ \frac{N_1}{N_0} = \frac{a_1v_1}{a_0v_0} $, donde $N_0$, $a_0$, y $v_0$ son respectivamente eficiencia, aceleración y velocidad máxima cuando se consume carbón; $N_1$, $a_1$, y $v_1$ son los mismos parámetros consumiendo un combustible determinado.
Entonces, la eficiencia del combustible dividida por la eficiencia del carbón es exactamente igual a la nueva velocidad máxima multiplicada por la nueva aceleración, lo que significa que el combustible nuclear es $ 1,15 \times 2,5 = 2,875 $ veces más eficiente que el carbón. Dado que las locomotoras pueden funcionar con cualquier combustible, es seguro asumir que utilizan un motor térmico. Si este motor funciona de la manera más eficiente posible (según un ciclo de Carnot), su eficiencia es:
$ N = 1 - \frac{T_{c}}{T_{h}} $, donde $T_c$ es la temperatura absoluta del foco frío del motor (288.15 K; temperatura ambiente), y $T_h$ es la temperatura absoluta del foco caliente del motor(calentado por el combustible). Es razonable suponer que en Nauvis el carbón se quema en 165 °C (438.15 K), basado en la temperatura del vapor de la caldera. Esto significa que la eficiencia de un tren que funciona con carbón es:
$ N = 1 - \frac{288,15\mathrm{K}}{438.15\mathrm{K}} = 0,34 $
La eficiencia del combustible nuclear es 2,875 veces mayor (ver arriba), lo que significa que es igual a 0,98. Esto significa que:
$ 1 - \frac{288,15\mathrm{K}}{T} = 0,98 $
$ T = \frac{288,15\mathrm{K}}{1-0,98} = 18297,525\mathrm{K} = 18024,375\mathrm{°C} $
Por tanto, el combustible nuclear tiene una temperatura superior a 18,000°C. Curiosamente, si el vapor de la caldera estuviera sólo 3,68 grados más caliente, la eficiencia del combustible nuclear sería exactamente 1. Y si superara un poco los 168,68 ° C, la física comenzaría a romperse.
Sin embargo, ese no es un gran problema, porque todo ya está roto sin él. Por ejemplo…
Los objetos tienen densidades increíblemente bajas
Esta parte se basa en la publicación de Reddit de u/Maouitippitytappin sobre su viaje para encontrar la escala en Factorio. Para recapitular su publicación: conociendo el consumo energético de los hornos básicos. En base a la fundición de hierro podemos encontrar la masa de una sola plancha de hierro, que resulta ser de tan solo unos 40 gramos. Del mismo modo, una placa de cobre pesa unos 65 gramos. (Las fuentes pueden variar; es posible que obtenga resultados de búsqueda diferentes)
Sabiendo esto, podemos calcular que las materias primas necesarias para una sola locomotora pesan unos miserables 14,6 kg. Dado que la locomotora ocupa un volumen de aproximadamente 24 m3 (asumiendo que tiene 2 m de altura según su apariencia), tiene una densidad de 0,6 kg/m3, que es aproximadamente la mitad de denso que el aire. ¡Esto significa que las locomotoras se pueden usar como globos!

Quizás Nauvis realmente está girando, y lo hace lo suficientemente rápido como para que la flotabilidad actúe hacia abajo debido a la fuerza centrífuga. Esta es una muy buena explicación de cómo se pueden colocar 240 locomotoras en un cofre de 1 m3; es porque probablemente sean plegables. Sin embargo, lo que no explica es como los trenes pueden girar con solo 12 metros de radio mientras se mueven a poco menos de 300 km/h sin descarrilarse. Deberían experimentar casi 60 g de aceleración al girar a toda velocidad:
$ a = \frac{v^2}{r} = \frac{(82,8\mathrm{m/s})^2}{12\mathrm{m}} = 571,32\mathrm{m/s^2} = 58,26g $
Dado que los railes claramente no están inclinados, los trenes deben tener ruedas de montaña rusa, sujetándose las vías por 3 lados. Personalmente, disfruto mucho la idea de que los trenes de la montaña rusa con globos se muevan a una velocidad de 300 km/h con un motor de 18 000 °C, pero tal vez sea solo yo.
Archivos de Nauvis: Técnicas obsoletas stringweasel
A lo largo de los años, Factorio ha cambiado significativamente. Nuevos jugadores, nuevas mecánicas, nuevos desarrolladores, nuevas estrategias, etc. Y a medida que las cosas cambian, algunas técnicas de juego quedan atrás para dar paso a formas nuevas y mejoradas. Como hace mucho tiempo cuando [Kerbals] (https://www.kerbalspaceprogram.com/) aterrizó en la Muna usando solo alas como tren de aterrizaje, o los jugadores de Minecraft construyeron boosters de minecart para impulsar sus carros. Hay viejos rituales y técnicas que ya no usamos en la era moderna. Siempre encuentro interesante mirar hacia atrás y ver lo que se hizo en el pasado, así que eso es lo que investigaremos aquí.
Postes de la victoria
En los días anteriores a la 0.13, los biters tenían mucho miedo de cualquier estructura que construyeras. Ni siquiera intentaban expandirse y crear nuevos nidos cerca de cualquier cosa que fuera colocada por un ingeniero. Esto resultó en un cierto ritual inventado por la comunidad: la colocación de los postes de la victoria. Simplemente podría colocar cualquier entidad después de limpiar un nido de nativos, generalmente algo barato como un cofre de madera o un poste eléctrico, y eso mantendría a los biters fuera de tu tierra legítimamente conquistada. Hay un gran video de NegativeRoot que explica este ritual. Irónicamente, después de 0.13, cuando los biters ya no tenían miedo de nuestras estructuras, algunos ingenieros desprevenidos encontraron nidos de biters dentro de sus bases indefensas.

Pérdida de compresión en las curvas
La mayoría no se dará cuenta, pero la cinta transportadora es la entidad más compleja en Factorio. Hoy en día “simplemente funciona”, pero tomó años solucionar todos los errores y dolores de cabeza. Cosas como elementos que se atascan, insertadores que no recogen el último elemento de la cinta y requieren cintas subterráneas para aumentar los UPS. Más infame, pero olvidada hace mucho tiempo, es la pérdida de compresión en las esquinas de antes de 0.12 y las técnicas utilizadas para mantener el 100% del rendimiento.
En ese entonces, las perdían la compresión en las esquinas debido a cómo se manejaban las colisiones. En el momento, los elementos de las cintas eran entidades individuales con cajas de colisión que provocaban que chocaran entre sí en las esquinas sin querer; hoy en día, estos artículos no tienen cajas de colisión en absoluto. Incluso en ese momento, los jugadores todavía querían construir a lo grande, por supuesto, y por eso tuvieron que sortear esta pérdida de compresión. Para construcciones más pequeñas, Se logró una compresión del ~100% reemplazando la esquina con una cinta de un nivel superior o usando dos divisores. Pero para las fábricas más grandes con buses grandes, donde las cintas ya eran del nivel más alto, se requerían diseños más complejos. Normalmente, estos diseños fueron hechos por el legendario mago de las cintas MadZuri, que se implementarían en las locas fábricas de ColonelWill.
Se tuvieron debates largos sobre como debería ser el comportamiento en las esquinas, incluso después de que la pérdida de compresión se corrigiera en 0.12. Si los elementos se mueven a una velocidad constante, como lo hacen actualmente, ¿lo que significa que los elementos internos salen primero de la esquina? ¿O el carril interior debería moverse más lento para que los carriles interior y exterior permanezcan sincronizados en las esquinas? Básicamente, esto se redujo a discutir el realismo frente al juego y, a veces sin darse cuenta, la latencia frente al rendimiento. Algunos simplemente disfrutaron todos los videos que se publicaron de líneas de producción reales dando vueltas en las esquinas.
La mecánica de las cintas transportadoras es una de esas cosas en las que, si no es perfecta, todos notarán que algo anda mal. Pero en cuanto funcione, pasará casi desapercibido por su intuición y sencillez. Esto se debe a que una buena implementación debe sentirse intuitiva y ocultar la enorme complejidad detrás de ella con una interfaz simple. Y, como saben, los ingenieros de hoy no suelen comentar sobre la mecánica de las correas. Las correas de transporte son fáciles de usar y tienen sentido. Esto significa que el equipo de Factorio realmente ha tenido éxito en la creación de la última implementación de cinta de transporte.
Divisores de prioridad manuales
Los divisores solo obtuvieron la capacidad de establecer una entrada/salida con prioridad en 0.16.17 (junto con la introducción del filtrado). Antes de esto, los divisores de prioridad tenían que construirse usando solo ingenio, espaguetis y muchos circuitos. Esto resultó en un período en 2016 en el que estos diseños fueron un tema candente en la comunidad. Jugadores como Steejo, raspi, canidae y Captain Konzept, por nombrar algunos, rápidamente se inició una investigación en profundidad y pruebas exhaustivas por el bien de la fábrica.

La construcción de un divisor de prioridad utilizando una red de circuitos no fue fácil, especialmente en ese momento, pero esto no detuvo a nuestra comunidad altamente capacitada; superaron numerosos obstáculos con vigor. Por ejemplo, al leer un cinturón completamente comprimido, podría mostrar 6 u 8 elementos aparentemente al azar. Peor aún, no hay forma de diferenciar una correa completamente comprimida de una correa con espacios. En cualquier caso, la red del circuito aún leería 8 (¡o 6!) Elementos en el cinturón. Esto resultó en varios diseños complicados, cada uno con sus propios trucos y trucos implementados por expertos para que funcionen. Captain Konzept hizo un gran video explicando los diversos enfoques de diferentes jugadores (y otro video comparando posteriormente estos diseños con los nuevos divisores con configuración de prioridad interna).
Después de un tiempo, la gente se dio cuenta de que en la mayoría de los casos un divisor de prioridad complejo no es realmente necesario, y se podría decir que un equilibrado adecuado es suficientemente bueno. Esta mentalidad cambió de nuevo después de que se lanzaron los divisores actualizados con la 0.16.17. De cualquier manera, el punto es que lograron crear un divisor de prioridad manual. Sin embargo, esta no es la única locura que los expertos lograron utilizando una mecánica de división simple.
Magia negra: filtrado mecánico del divisor
Como se mencionó, los divisores anteriores a la 0.16.17 (o 0.16.16) se comportaban de manera diferente y no tenían configuración de filtro. Sin embargo, esta limitación no impidió que la comunidad abusara de los divisores para filtrar elementos de todos modos, ¡esta vez sin usar circuitos! Comenzó con esta publicación de SPolygon diciendo que su divisor no estaba dividiendo correctamente. Como explicó daniel34, el divisor también elige a que lado se dirige un elemento según el tipo de elemento, no simplemente alternando después de cada elemento. Esto despertó la curiosidad del legendario XKnight que inmediatamente se le ocurrieron algunos prototipos que abusan de esta mecánica. ¡Estos diseños parecían estar al borde de la magia e incluso asombraron a los desarrolladores! Aproximadamente un año después, u/tzwaan redescubrió el trabajo de XKnight, continuó la investigación, y luego se lo mostró al mundo de Reddit, denominándolo un clasificador de elementos de Magia Negra.
Debe recordarse que estos divisores no tienen capacidad de filtrado prevista. Aún así, los expertos de la comunidad podrían lograr el filtrado abusando de su mecánica inherente. En ese entonces, en 2016 y 2017, la mayor parte de la comunidad estaba obsesionada con los divisores, ya sea la división de prioridades o el filtrado loco de magia negra. Y en lugar de quejarse a los desarrolladores para que agreguen estas mecánicas como características, trabajaron juntos para resolver estos problemas comunes simplemente jugando. En mi opinión, es un testimonio de lo grandiosa que puede ser la comunidad de Factorio y lo dedicados y hábiles que son algunos de nuestros jugadores.
Contribuir
Como siempre, buscamos personas que quieran contribuir con Alt-F4, ya sea enviando un artículo o ayudando con la traducción. Si tienes algo interesante en mente que quieres compartir con la comunidad de una manera pulida, este es el lugar para hacerlo. Si no estás muy seguro, con gusto te ayudaremos discutiendo ideas de contenido y preguntas sobre la estructura. Si eso te parece algo que te guste, únete a Discord para comenzar.