Alt-F4 #23 – Extravagante Fließbänder 12.02.2021
übersetzt von EDLEXUS, lektoriert von dexteritas, Nanogamer7

Inhaltsverzeichnis
Nach einer zweiwöchigen Pause aufgrund einiger druckfrischer FFFs, sind wir diese Woche mit zwei Artikeln rund um das Thema Fließbänder zurück. In dem ersten erforscht Recon419A ein interessantes Konzept, bei dem die Fließbänder Gegenstände just-in-time liefern. Danach wird es mit einem tiefen Blick in den Aufbau einer Turing-Maschine nur mit Fließbändern von Pocarski richtig nerdig. Informatik-Abschluss empfohlen!
Logistikbänder Recon419A
In Factorio gibt es drei Wege, um Gegenstände zu transportieren: Förderbänder, Roboter und Züge. Förderbänder eignen sich gut für den Transport von ein oder zwei verschiedenen Gegenstandstypen, Züge sind optimal für große Mengen eines Gegenstände und Roboter für komplizierte Fertigungsaufgaben. Manchmal braucht man aber eine Kombination dieser Eigenschaften, wo dann Systeme wie Sushibänder zum Einsatz kommen. In diesem Artikel möchte ich einen anderen Ansatz vorstellen, den ich „logistics belts“ (zu Deutsch: Logistikbänder) nenne. Wie Sushibänder können Logistikbänder auch mit Mods verwendet werden, und sind selbst kein Mod, sondern eher ein Weg, um mit einigen einfachen Schaltungen und Förderbändern Gegenstände zu verteilen. Das Ziel ist es, Gegenstände effektiver an ihr Ziel zu bringen, so wie es im Vanilla-Logistiknetz oder im Schienennetz mit Mods wie LTN der Fall ist.
Das Konzept von Logistikbändern
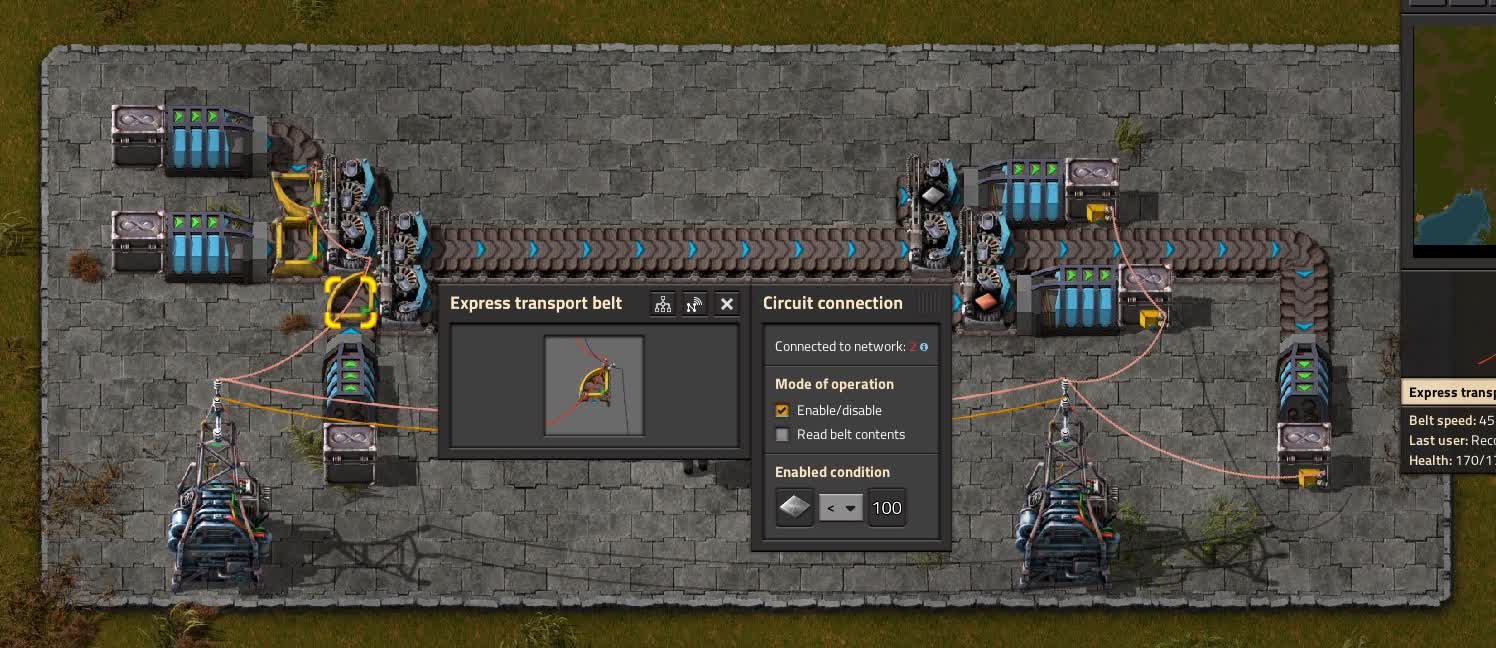
Logistikbänder sind ein etwas komplexeres Konzept, aber einfacher zu verstehen, wenn man sich eins in Aktion anschaut. In diesem Beispiel ist zu beachten, dass mehrere Gegenstände auf dem selben Förderband befinden, und jeweils nur auf das Band umgeladen werden, das sie aktuell anfordert. Wenn nur Eisen und Kupfer benötigt werden, wird kein Stahl geschickt, wenn nichts benötigt wird bleibt das Band leer.
In diesem Beispiel ist zu sehen, dass eine Nachricht für Nachschub in der Schaltung gesendet wird, wenn am Zielort weniger als 100 Gegenstände vorhanden sind. In der Realität hat die Länge des Bandes Einfluss darauf, wie viele Gegenstände nachgefordert werden. Wenn das Förderband sehr lang ist, werden 100 Stück am Zielpunkt vorgehalten und hunderte weitere noch auf den Bändern. Es gibt ein theoretisches Limit wie viele Gegenstände vorgehalten werden können, ohne die Empfangskiste zu überfüllen, diese Grenze ist aber in der Realität mit Stahlkisten fast nicht zu erreichen, da für sehr lange Strecken sowieso Züge zum Einsatz kommen. Falls du selber mal mit diesem Konzept rumspielen möchtest, findest du hier die Blaupause, es ist aber zu beachten, dass die Blaupause die Belader von Loader Redux benötigt.
Verwendungen für Logistikbänder
Logistikbänder sind sinnvoll, wenn viele Gegenstände auf einmal benötigt, aber nur für eine kurze Zeit benötigt werden. Jeder der schonmal Fließbänder mit Robotern automatisiert hat, kennt die Wolke an Robotern beim erstmaligen Anschalten der Anlage, wenn etwa zehntausend Zahnräder und 1500 elektronische Schaltkreise angefordert werden. Auch beim Versuch ein Nuklearreaktor oder ein Raketensilo zu bauen bildet sich um die Montagemaschine eine Wolke, da die Anlage nicht auf so einen Andrang vorbereitet ist. Wenn eine große Stückzahl Gegenstände benötigt wird, ist es einfacher ein Fließband zu legen, dort werden zehntausend Zahnräder in unter vier Minuten transportiert, und das ohne spürbaren UPS-Einbruch. Währenddessen benötigen Roboter 2500 Einzelflüge und überlasten dabei vollständig die Ladeinfrastruktur, die nie für so einen Andrang entworfen wurde, und es dauert lange, bis das gesamte System wieder vollständig einsatzbereit ist. Dedizierte Fließbänder für jeden Gegenstandstyp kommen aber mit ganz eigenen Problemen. Die meiste Zeit stehen die Bänder still und nehmen nur Platz in der Fabrik weg, falls dieser Platz überhaupt vorhanden ist. Für Logistikbänder ist es trivial, eine große Zahl Zahnräder vermischt mit einigen elektronischen Schaltkreisen zur Fließbandproduktion zu versenden, wo dann die Verteilung mit Robotern erfolgen kann.
Limitierender Faktor: mehrere Ziele
Das Problem, Gegenstände des gleichen Typs zur selben Zeit zu mehreren verschiedenen Zielen zu transportieren ist nicht trivial, und stellt ein Problem dar, was ich bis jetzt nicht lösen kann. Da filternde Teile immer alle Gegenstände eines Typs ausfiltern, sind komplizierte Schaltungen mit mehreren Eingangssignalen von verschiedenen Orten und komplexe Teilersysteme nötig. Ich habe mich lange mit diesem Problem beschäftigt, und obwohl ich mehrere Prototypen entwickelt habe, sind sie alle anfällig für Verstopfungen oder eine falsche Verteilung der Gegenstände. So wie ich die Factoriocommunity kenne, würde es mich nicht wundern, wenn dieses Problem innerhalb von ein oder zwei Wochen auf verschiedene Arten gelöst ist. Vielleicht hören wir ja von deiner Lösung in einer zukünftigen Ausgabe von Alt-F4. Für jetzt überlasse ich das aber als Challenge für die Community. Ich würde mich freuen, von deiner Lösung zu hören.
Gedanken zu Sushibändern
Spieler, die sich schon lange mit dem Spiel beschäftigen, werden schon mal von einem ähnlichen Konzept gehört haben: Sushibänder. Wie Logistikbänder transportieren auch Sushibänder mehr als zwei Rohstoffe auf einem Band, allerdings meistens als Kreislauf für komplexe Craftinganwendungen. Eine Schaltung am Eingang hilft dabei, die Menge eines Gegenstände auf dem Band zu kontrollieren, was zu komplizierten Systemen wie dem „Bloodbus“ führen kann, einem Kreislaufsystem für die gesamte Fabrik. Das System der Logistikbänder ist zwar ähnlich, unterscheidet sich aber grundlegend in einigen Aspekten. Der Hauptunterschied ist im Grunddesign: Während Sushibänder im Kreis laufen und in keiner bestimmten Reinfolge Montagemaschinen beliefern, transportieren Logistikbänder Gegenstände zielgerichtet von einem Ort zum andern. Es ist sogar möglich, Logistikbänder statt einem normalen Bussystem zu verwenden, um Sushibänder zu befüllen. Wenn Rohstoffe benötigt werden, werden sie in genauer Stückzahl gesendet, mit Schaltungen, die präzise die Überbelegung des Kreislaufes verhindern. Andere Konzepte, wie Urwerkbänder oder Greiferlimitierende Systeme können mit Logistikbändern kombiniert werden und so zum Maximum an Ingenieurskunst führen. Meiner Meinung nach sind Logistikbänder nur ein weiteres Werkzeug im Werkzeugkasten des Spielers.
Fließbandbasierter Rechner, Teil 1: Nicht ganz so schnelle Mathematik pocarski
In Factorio können wir das Schaltungsnetzwerk verwenden, um Systeme verschiedener Komplexität zu bauen. Von einfacher Boolescher Logik bis hin zu vollständigen Computern, manch einer ist auch verrückt genug, DOOM drauf zu spielen. Was aber nicht ganz offensichtlich ist, ist dass das Schaltungsnetzwerk nicht das einzige Turing-Vollständige System ist (falls du dir unsicher bist, was das bedeutet, schau dir mal den Link an). Tatsächlich kann man einen Computer aus etwas sehr einfachem bauen, etwas, auf das man fast von Anfang an Zugriff hat: Fließbänder.
In dieser zweiteiligen Serie werde ich erklären, wie man zwei Systeme, welche in realen Computern verwendet werden, konstruiert, und das nur mit Fließbändern und Teilern. Ich werde Belader und Unendlichkeitskisten verwenden, aber es verlassen immer genauso viele Gegenstände das System wie zugeführt werden, so das die Bänder auch durch ein Zwischenlager zurückgeführt werden könnten. Ich habe mich aber dagegen entschieden und ein kompakteres System mit weniger Spaghetti entworfen. Ich muss mich an dieser Stelle bei letao12 bedanken, der eine Videoserie zur Konstruktion einer Förderbandbasierten CPU gemacht hat und mich inspirierte, diese Idee noch einmal selbst aufzugreifen.
Damit ein System Turing-Vollständig ist, muss es sogenannte Logikgatter ermöglichen. Logikgatter sind einfache Elemente, die grundlegende Boolesche Algebra berechnen, indem sie aufgrund ihrer aktuellen Inputs ein Output ausgeben. Es gibt nur zwei Zahlen in Boolescher Algebra: 1 und 0. In der Elektronik werden sie mit einer hohen und einer niedrigen Spannung realisiert, aber in unserem Fall wollen wir uns darauf verständigen, das ein Förderband mit Gegenstände eine 1 darstellt und ein leeres Förderband eine 0. Es gibt drei grundlegende logische Gatter:
- ODER-Gatter – Ausgang ist 1, wenn mindestens ein Eingang 1 ist
- UND-Gatter – Ausgang ist 1, wenn alle Eingänge 1 sind
- NICHT-Gatter – Ausgang ist 1 genau dann, wenn der Eingang 0 ist
Die Wahrheitswerttabelle unten zeigt die dazugehörigen Ausgänge in Bezug zu den möglichen Eingängen.
| A | B | NICHT A | A ODER B | A UND B |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 |
Es ist bekannt, dass es durch Verkettung dieser Gatter (manchmal mit Schleifenbildung einiger Verbindungen) möglich ist, eine Turingmaschine zu konstruieren. Alle drei dieser einfachen Logikgatter können komplett mit Fließbändern und Teilern realisiert werden. Hier ist ein Link zum Blaupausenbuch mit Blaupausen von allem, was in diesem Artikel behandelt wird, für den Fall, dass jemand noch selbst etwas damit rumexperimentieren möchte. Ich werde verschiedene Gegenstände ab sofort mit „GegenstandTyp 1 / 2 / 3 / …“ bezeichnen und die Prioritäts / Nicht-Prioritäts Ein- und Ausgänge als „primär / sekundär“, hauptsächlich für Übersichtlichkeit und Praktikabilität. Ich werde auch in den Bildern verschiedene Farben verwenden, um zwischen Gegenstandstypen zu unterscheiden.
Die grundlegenden Gatter
Das UND und ODER Gatter bestehen ganz einfach nur aus einem einzelnen Teiler mit eingestellter Priorität:
Das NICHT-Gatter ist etwas schwieriger, kann aber mit mehr als einem Gegenstandstyp und einigen cleveren Filtern und Prioritäten realisiert werden:
Während Eingang A 0 ist, bekommt der erste Teiler nur einen Eingangswert, und so ist Gegenstandstyp 2 auf dem primären Ausgang, also ist der NICHT-A-Ausgang 1. Wenn Eingang A 1 ist, bekommt der erste Teiler nun zwei Eingabewerte, Gegenstandstyp 1 geht in den Primäreingang und somit auch auf den Primärausgang, wo es Gegenstandstyp 2 ersetzt, welches jetzt den sekundären Ausgang belegt. Der Sekundärausgang ist im Prinzip eine Kopie von A, allerdings mit einem anderen Gegenstandstyp.
Der Primärausgang des ersten Splitters ist immer 1, ändert aber den Gegenstandstyp in Abhängigkeit von der Eingabe. Mithilfe eines filternden Teilers können wir nun den Ausgang auf zwei Wege aufteilen: ein Weg wird einfach nur Signal A sein, mit dem selben Gegenstandstyp wie der Originaleingang, während der andere Weg NICHT-A ist, allerdings mit Gegenstandstyp 2.
Dieses zweite System ist besonders praktisch, da es ein NICHT-Gatter, ein Signalduplikator und einen Gegenstandstauscher kombiniert. Wir benötigen Signalduplikatoren, da das Aufteilen von Bändern mit Teilern den Gegenstandsdurchfluss verändert, und nicht volle Bänder anders mit Teilern interagieren und weder eine 1 noch eine 0 darstellen. Wir benötigen auch Gegenstandstauscher, da es oft eine Diskrepanz zwischen dem Ausgangstyp eines Gatters und dem Eingangstyp eines anderen gibt.
Der Halbaddierer
Jetzt, da wir unsere drei Basiskomponenten zusammen haben, können wir einen Halbaddierer bauen. Aber warum brauchen wir einen Halbaddierer? Nunja, wie der Name schon erkennen lässt, ein Halbaddierer ist eine Hälte eines Volladdierers, was eine Schaltung darstellt, welche Binärzahlen addieren kann. Das ermöglicht uns die Addition, und wenn man beim addieren kreativ ist, dann kann man auch jede andere vorstellbare mathematische Operation durchführen.
Der Halbaddierer ist eine Schaltung, welche zwei 1 Bit große Binärzahlen addiert. Das mag kompliziert klingen, ist aber am Ende relativ simpel. Beide Eingänge A und B sind 1 Bit große Binärzahlen, was bedeutet, das der maximale Ausgabewert 2 (1+1) ist. Das passt unvorteilhafter Weise aber nicht mehr in einen 1 Bit großen Ausgang. Stattdessen werden wir eine 2 Bit große Binärzahl verwenden, wo die erste Stelle den Wert 2 (21) hat und die zweite Stelle den Wert 1 (20). Wenn man das beachtet, kommt man auf diese Wahrheitstabelle:
| A | B | Erste Stelle von A + B | Zweite Stelle von A + B |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Wie man sehen kann ist die erste Stelle einfach nur A UND B. Für die zweite Stelle benötigt man allerdings ein sogenanntes XOR-Gatter (XOR steht für Exklusiv Oder). Ein XOR-Gatter hat einen Ausgang von 1, wenn genau einer der Eingabewerte 1 ist, was genau das ist, was wir für die zweite Stelle brauchen.
Die XOR-Gatterlogik ist „A oder B, aber nicht beide“, und lässt sich deshalb zusammensetzen als (A ODER B) UND NICHT (A UND B) So würde man das mit den oben beschriebenen Logikgattern lösen:
Zu beachten ist, dass wir den UND-Gatter-Ausgang durch die Kombination des Duplikator-NICHT-Gatters mit dazu bekommen, was uns einen kompletten Halbaddierer gibt. Praktischerweise können wir den ersten Gegenstandstauscher mit dem zweiten UND-Gatter kombinieren, was uns ermöglicht, einen Teiler zu sparen:
Das Endprodukt
Um jetzt aus unserem Halbaddierer einen Volladdierer zu machen, kombinieren wir zwei von ihnen hintereinander (daher der Name „Halbaddierer“):
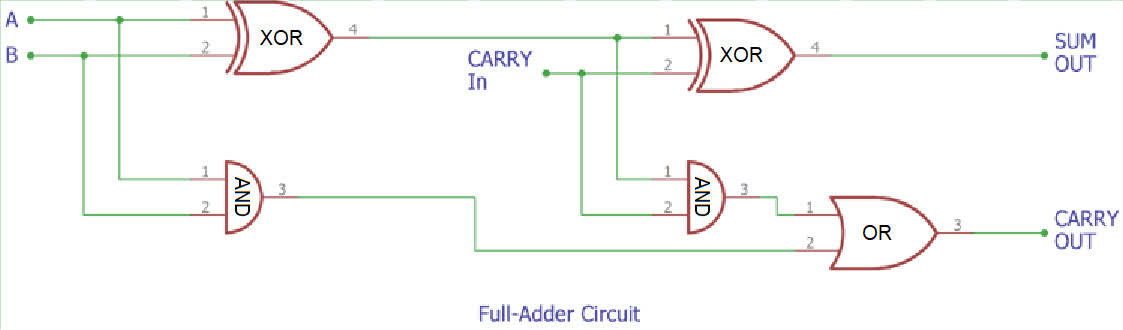
Wie zu erkennen ist, ein Volladdierer ist nur zwei Halbaddierer hintereinandergeschaltet. Wir könnten jetzt einfach den Schaltkreis kopieren, aber durch die besonderen Eigenschaften von Fließbändern haben wir einen viel besseren und einfacheren Weg. Die zwei Seiten eines Förderbandes werden von den Teilern unabhängig voneinander behandelt, was bedeutete, das wir anstatt zwei Halbaddierer zu verknüpfen, wir alles einfach zweimal durch den selben Halbaddierer laufen lassen können. Das ist im Normalfall mit traditionellen Logikgattern unmöglich, aber in der spannenden neuen Welt von Factorio ist alles möglich. Hier ist wie so etwas aussehen würde:
Hier verwendet der erste Halbaddierer die rechte Seite des Förderbandes, und der zweite Halbaddierer die linke Seite. Zuerst wandern die Eingabewerte ganz normal durch den ersten Halbaddierer auf der rechten Bandseite. Danach wird der XOR-Ausgang des Halbaddierers zurück an den Anfang gebracht und kommt jetzt auf die linke Seite des Förderbandes. Er geht wieder durch die selbe Mechanik wie vorher, da er aber jetzt auf der anderen Seite ist findet keine Interaktion statt. Der zweite Halbaddierer hat allerdings immer noch einen freien Eingang, und so müssen wir noch ein drittes Eingabeband verbinden, das sogenannte Übertragseingabebit. Die UND-Ausgänge beider Halbaddierer werden von der Seite auf ein Band geladen und wirken somit automatisch als ODER. Interne Verzögerungen können dazu führen, das beide Halbaddierer-Übertragsausgänge zur selben Zeit einen Ausgangswert haben, und so versucht wird, ein volles Band auf ein halbes Band zu entladen. Deshalb benötigen wir ein Überflussschutz, damit das Übertragsbit nicht den ganzen Mechanismus verstopft. Nach etwas Umstrukturierung kommen wir dann dazu:
Das ist exakt die selbe Schaltung wie das vorherige Bild, und ich lasse es als eine Übung für den Leser das zu verifizieren. Das einzige was jetzt noch fehlt ist es, viele Halbaddierer zusammenzuschalten und einige Berechnungen durchführen zu lassen. Deshalb ist hier ein ausschließlich aus Fließbändern bestehender Additionsrechner, welcher 01001101 (77) + 10001011 (139) = 011011000 (216) berechnet:
Zahlen addieren mach zwar Spaß, hat aber noch nichts mit irgendeiner Art von Speicher zu tun, was genau das ist, was wir uns in der nächsten Ausgabe anschauen werden. Bleibt gespannt!
Beitragen
Wie immer suchen wir nach Leuten, die zu Alt-F4 beitragen wollen, sei es mit einem Artikel oder durch Hilfe bei Übersetzungen. Wenn du etwas Interessantes im Kopf hast, das du mit der Community in einer eleganten Art teilen möchtest, hier kannst du das tun. Falls du dir unsicher bist, beantworten wir gerne Fragen zu Inhalt und Struktur. Falls das nach etwas klingt, woran du interessiert bist, tritt unserem Discord bei, um es nicht zu verpassen!