Alt-F4 n°47 - Optimiser la solution 17-09-2021
traduit par bev, Firerazer
Sommaire
-
Optimiser la Solution
ilbJanissary - Pourquoi utiliser un calculateur ?
- Concepts
- Vitesse de fabrication
- Équations de recettes
- Matrices de recettes
- Programmation linéaire
- Pourquoi avons-nous besoin d’une fonction de coût ?
- Comment définir une fonction de coût ?
- Problème dual de minimisation
- Résolution avec le simplexe
- Onglet Matrice
- Informations sur les résultats
- Modificateurs de coûts
- Tableau canonique simplexe et solution
- Algorithmes alternatifs
- Résumé rapide
- Contribuer
Après trois semaines de coupure, Alt-F4 est de retour, plus motivé que jamais ! On commence par un gros boom avec ilbJanissary qui nous emmène dans les profondeurs des méthodes de calculs qui se cachent derrière FactorioLab, là où se trouve sa magie. Cela peut sembler complexe à première vue, mais le processus vous est présenté petit à petit et illustré avec des exemples à propos. Aucun regard ne sera glacé par la lecture de cet article (espérons-le !).
Optimiser la Solution ilbJanissary
Salut ! En tant que développeur Angular et utilisateur de longue date du calculateur Factorio de Kirk McDonald, j’ai décidé en 2020 de construire mon propre calculateur en ligne pour les jeux de construction d’usine, appelé FactorioLab. Kirk McDonald a publié un document sur son approche qui m’a aidé à démarrer, mais il s’arrête avant d’expliquer l’algorithme qu’il utilise pour trouver une solution. Après avoir lutté contre les mathématiques pendant un certain temps et construit deux itérations de résolveurs non-simplex dans FactorioLab, je désirais partager avec la communauté ce que j’ai appris en implémentant un vrai résolveur d’algorithme simplex. Un résumé rapide se trouve tout en bas de l’article.
Pourquoi utiliser un calculateur ?
Commençons par le début. Dans les jeux de construction d’usine comme Factorio, Dyson Sphere Program, et Satisfactory, l’objectif est d’extraire des ressources brutes, d’utiliser ces ressources pour fabriquer des objets en suivant une recette, et d’utiliser ces objets pour découvrir des objets et des recettes plus avancés. Au début, les recettes et les objets concernés sont simples et ne nécessitent pas une planification approfondie, mais au fur et à mesure que l’on débloque des objets et des recettes, la chaîne de production peut devenir incroyablement compliquée. Les calculateurs d’usine comme FactorioLab et le calculateur Factorio de Kirk McDonald ont pour but d’aider à déterminer combien de ressources brutes et d’usines sont nécessaires pour produire durablement des objets à un certain débit.
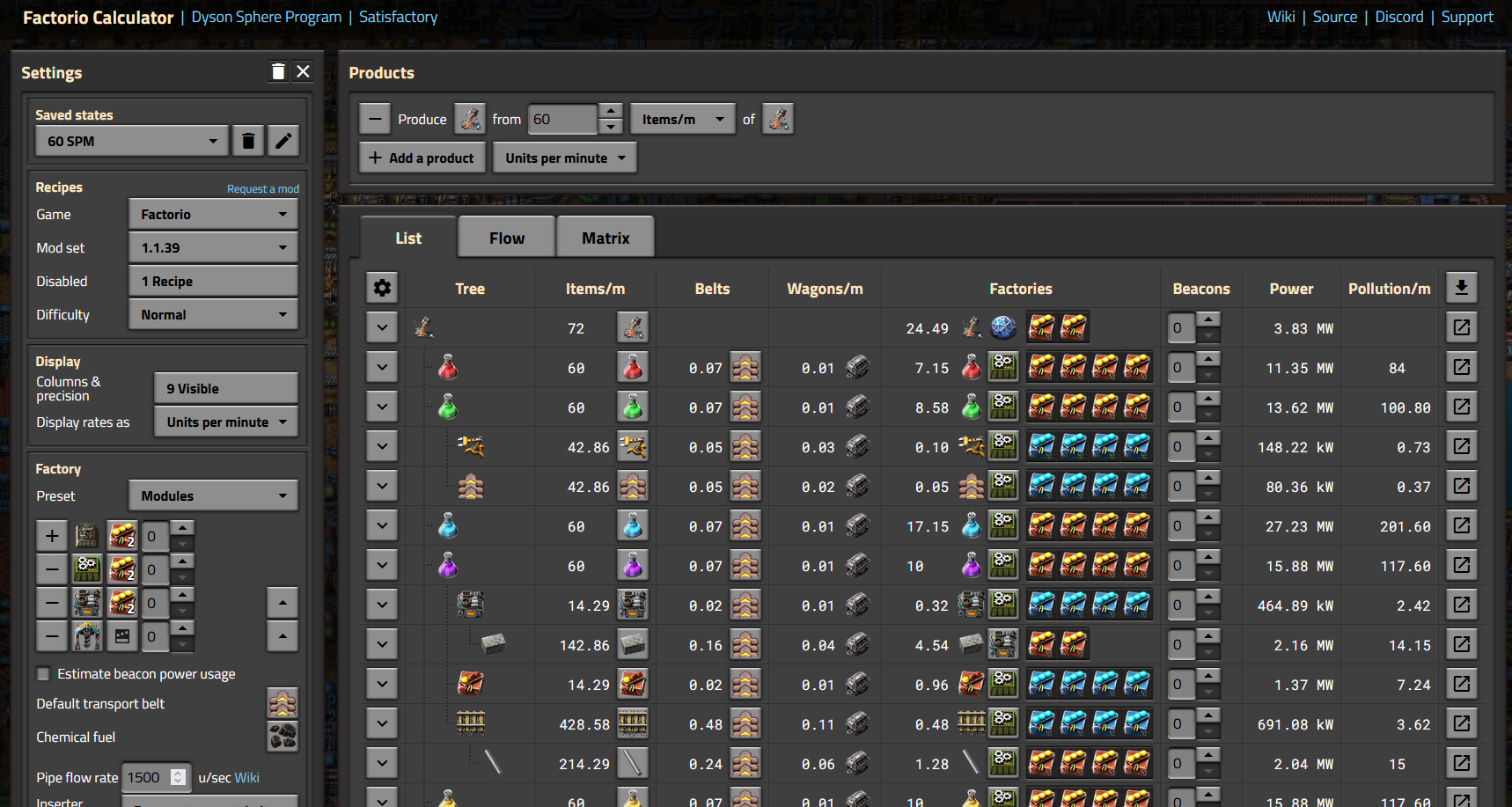
Concepts
Il y a deux concepts importants dans les jeux de construction d’usine qui sont importants pour comprendre les mathématiques derrière les calculs : les objets et les recettes.
- Les objets sont les produits et les ingrédients des usines. Certains objets ne sont que des intermédiaires et ne peuvent rien faire par eux-mêmes, comme la plupart des ressources brutes. D’autres peuvent également servir à quelque chose dans le jeu, comme le carburant, les convoyeurs, les fours, les machines d’assemblage, la production et la distribution d’énergie, etc.
- Les recettes sont les moyens par lesquels les joueurs fabriquent de nouveaux objets plus avancés dans le jeu. Certains objets peuvent être fabriqués à la main à l’aide de la recette, tandis que d’autres recettes ne peuvent être exécutées que par des bâtiments spécifiques, comme les machines d’assemblage ou les fours. Les recettes prennent généralement un ensemble spécifique d’objets comme ingrédients, prennent un certain temps pour être exécutées, et produisent un ensemble donné d’objets comme produits. Les recettes sont souvent représentées par une liste d’ingrédients et un temps d’exécution à gauche d’une flèche, qui pointe vers la liste des produits à droite.
Par exemple, dans Factorio, un objet de base est le Minerai de fer. Le Minerai de fer est une ressource brute, ce qui signifie qu’il est produit par une recette qui ne prend aucun objet en entrée :
Cette recette peut être effectuée sur un gisement de Minerai de fer, à la main ou à l’aide d’une foreuse. Le Minerai de fer est principalement utilisé comme ingrédient pour produire des Plaques de fer, qui utilisent leur propre recette :
Les Plaques de fer ne peuvent pas être fabriquées à la main, et doivent être produites dans un four. Les recettes peuvent également inclure de nombreux ingrédients et résultats, comme l’une des recettes les plus complexes de Factorio, le Raffinage avancé:
Cette recette ne peut être fabriquée qu’à l’aide d’une 
Raffinerie.
Vitesse de fabrication
Le temps réel de fabrication d’une recette est également affecté par la vitesse de fabrication de la machine utilisée pour cette recette. Par exemple, la 
Foreuse électrique a une vitesse de fabrication de 0,5, ce qui signifie que lorsqu’elle est utilisée pour extraire du Minerai de fer en utilisant la recette ci-dessus, il faut en fait deux secondes par Minerai de fer. Pour simplifier, nous considérerons généralement que la vitesse de fabrication sera ici fixée à 1.
Équations de recettes
Vous remarquerez peut-être que si vous remplacez la flèche par un signe égal, la recette peut facilement être interprétée comme une équation. Le temps n’étant pas un élément réel, pour que cette équation ait un sens, nous devons diviser les deux côtés par la durée et donc traiter les chiffres de l’équation comme des débits au lieu d’un simple nombre d’objets. Ainsi, la recette du Minerai de fer devient :
Dans ce cas, le côté gauche est égal à zéro puisque la recette ne prend aucune entrée. De même, la recette de la Plaque de fer devient :
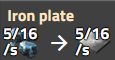
Jusqu’à un certain point, ces équations sont relativement simples à résoudre. De nombreux objets ne peuvent être produits que par une seule recette, et il suffit donc d’une simple opération d’algèbre pour déterminer le nombre d’objets et de recettes nécessaires pour produire des objets selon un certain débit. Dans FactorioLab, si les produits requis ne peuvent être fabriqués que par une seule recette, ces équations sont résolues directement le plus en aval possible de la chaîne de production. Cependant, certains objets peuvent être produits au moyen de plusieurs recettes différentes, ce qui rend plus complexe la détermination de la recette, ou souvent de la quantité de chaque recette, qui est optimale pour produire les objets souhaités tout en consommant le moins de ressources.
Matrices de recettes
Le problème canonique de Factorio est le Raffinage avancé et le Craquage, et sera utilisé comme exemple principal pour trouver une solution. Ce problème implique généralement au moins cinq recettes et cinq objets. Les recettes sont :
Pétrole brut (ressource brute)
La vitesse de production du Pétrole brut varie en fonction de la ressource sur la carte, mais peut être traitée de manière simplifiée.
Eau (ressource brute)
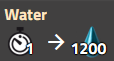
Raffinage avancé
Craquage du Pétrole lourd en Pétrole léger
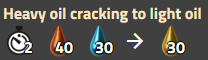
Craquage du Pétrole léger en Gaz de pétrole
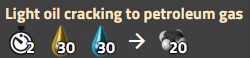
Notez que d’autres recettes peuvent également être impliquées, telles que le Raffinage de base et la Liquéfaction du charbon, mais elles seront ignorées pour le moment.
En divisant ces recettes par leur durée de fabrication, on obtient une équation basée sur les débits, qui est la forme dont le calculateur a besoin pour calculer les besoins de production. Puisque la vitesse de fabrication de toutes les usines impliquées ici est de 1, nous n’avons pas besoin de faire d’ajustements pour tenir compte de la vitesse de fabrication, mais cela serait nécessaire pour de nombreuses autres usines, ou à chaque fois que des modules ou des diffuseurs sont impliqués.
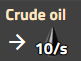
Pétrole brut (ressource brute)
Eau (ressource brute)
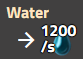
Raffinage avancé
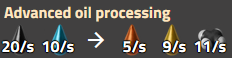
Craquage du Pétrole lourd en Pétrole léger
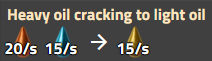
Craquage du Pétrole léger en Gaz de pétrole
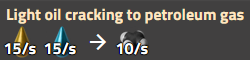
Ces recettes peuvent être organisées dans une matrice. Cette matrice doit comporter des colonnes pour les recettes et des lignes pour les objets. Cela crée un ensemble différent d’équations, une équation pour chaque objet. Par exemple, pour le pétrole brut : 10 - 20 = nombre de 
Après avoir divisé les quantités d’objets par leur temps de fabrication, la matrice complète se présente comme suit :
|
|
|
|
|
|
|---|---|---|---|---|---|
|
10 | 0 | -20 | 0 | 0 |
 |
0 | 1200 | -10 | -15 | -15 |
 |
0 | 0 | 5 | -20 | 0 |
 |
0 | 0 | 9 | 15 | -15 |
 |
0 | 0 | 11 | 0 | 10 |
Ensuite, nous devons tenir compte de ce que nous voulons produire réellement à partir de notre usine. Pour gérer cela, nous pouvons ajouter une colonne pour représenter les produits finaux de notre usine. Par exemple, disons que nous voulons produire 5 Pétrole lourd/seconde et 100 Gaz de pétrole/seconde. Afin de représenter cette idée dans la matrice, nous devons rendre ces valeurs négatives, car nous indiquons ainsi que nous retirons cette quantité du système.
|
|
|
|
|
Sort | |
|---|---|---|---|---|---|---|
|
10 | 0 | -20 | 0 | 0 | 0 |
|
0 | 1200 | -10 | -15 | -15 | 0 |
|
0 | 0 | 5 | -20 | 0 | -5 |
|
0 | 0 | 9 | 15 | -15 | 0 |
|
0 | 0 | 11 | 0 | 10 | -100 |
Programmation linéaire
Une matrice de cette nature est appelée un programme linéaire en mathématiques, et peut être résolue en utilisant des techniques de programmation linéaire. La méthode la plus courante pour résoudre un programme linéaire est l’Algorithme du simplexe, et c’est la méthode utilisée tant par FactorioLab que le calculateur Factorio de Kirk McDonald. Puisqu’il existe plusieurs solutions possibles à ce programme linéaire, l’algorithme du simplexe adopte l’approche consistant à maximiser une fonction objectif, qui est essentiellement une autre ligne de la matrice.
Même si nous n’avons pas nécessairement d’objectif à maximiser dans notre programme linéaire, nous voulons minimiser la quantité de ressources et d’usines nécessaires pour produire nos objets en sortie. Ainsi, au lieu d’ajouter un objectif que nous voulons maximiser, nous pouvons d’abord ajouter une fonction de “Coût” à notre programme linéaire afin de pouvoir décrire comment nous voulons minimiser le nombre de ressources et d’usines dans notre solution.
Pourquoi avons-nous besoin d’une fonction de coût ?
Pour les usines simples où il n’y a qu’une seule recette pour chaque usine, nous n’avons même pas besoin d’une fonction de coût. Nous pouvons calculer la quantité de chaque ingrédient dont nous avons besoin, et continuer à descendre dans la chaîne des recettes jusqu’à ce que nous trouvions une solution. Alors pourquoi le programme linéaire a-t-il besoin d’une fonction de coût ?
Regardons l’exemple du raffinage dans Factorio. Dans notre exemple, nous voulons produire du Gaz de pétrole et du Pétrole lourd. Notez que le Raffinage avancé permet déjà de fabriquer ces deux produits. Par conséquent, une solution valable consiste à ignorer complètement les recettes de craquage et à produire tous les produits pétroliers dont nous avons besoin directement à partir du Raffinage avancé. Alors, pourquoi utiliser le craquage dans Factorio ? Il y a deux raisons principales :
- L’équation n’est pas équilibrée, ce qui signifie que dans presque toutes les usines, les produits pétroliers en sortie ne correspondront pas aux débits des produits pétroliers souhaités, et finalement l’un d’entre eux remplira tout le stockage disponible et obligera la production à s’arrêter complètement. Dans la plupart des usines produisant uniquement des sciences, le coupable sera le Pétrole léger. Dans Factorio, il n’y a aucun moyen de simplement “brûler” l’excès, et vider manuellement les réservoirs de stockage est fastidieux.
- Elle utilise le Pétrole brut en excès. Le Pétrole brut n’est pas aussi facile à obtenir que l’eau, donc nous voulons généralement en minimiser la quantité nécessaire. En craquant l’excédent de Pétrole léger en Gaz de pétrole, nous pouvons à la fois traiter l’excédent de Pétrole léger et réduire la quantité de Pétrole brut nécessaire, au détriment d’un supplément d’ Eau, qui est plus facile à obtenir.
Une fonction de coût quantifie la difficulté d’obtention des ressources et l’effort nécessaire à la création d’usines. Une solution qui nécessite moins de ressources est meilleure qu’une solution qui nécessite beaucoup de ressources, et une solution qui nécessite moins d’usines est meilleure qu’une solution qui nécessite plus d’usines. En mettant des chiffres spécifiques sur le coût de l’obtention des ressources et de la mise en place des usines, nous pouvons directement quantifier le coût d’une solution, et le calculateur peut utiliser ce coût pour déterminer quelle solution est optimale.
Comment définir une fonction de coût ?
La fonction de coût peut être plutôt abstraite et arbitraire car il n’y a pas de coût déterminé des ressources et des usines dans des jeux comme Factorio et Dyson Sphere Program. Au lieu de cela, nous devons nous fier à notre intuition de ce qui est le plus difficile à obtenir et à mettre en place dans une usine. Dans FactorioLab, cela se résume à quelques variables particulières qui définissent la fonction de coût :
- Une seule usine exécutant une recette coûte 1.
- Une unité d’ Eau coûte 100, car l’eau est généralement facile à obtenir.
- Une unité de Pétrole brut coûte 1000, car il est généralement produit en plus grande quantité que les autres ressources minières.
- Une unité de ressources “minées” coûte 10 000. Dans Factorio, cela s’applique au Charbon, Minerai d’uranium, Pierre, Minerai de fer, et Minerai de cuivre. En général, ce sont les ressources que nous voulons minimiser le plus.
- Une unité de ressources “récoltées manuellement” coûte 100 000. Dans Factorio, cela s’applique par exemple au Bois. Bien que le Bois ne fasse généralement pas partie des recettes importantes dans le Factorio de base, nous voulons minimiser l’utilisation des ressources que nous ne pouvons pas collecter automatiquement.
Nous pouvons représenter cette fonction de coût comme une ligne supplémentaire dans notre matrice. Afin de prendre en compte de manière précise le coût des ressources exploitées, nous allons simplifier ces recettes afin que le coût soit basé sur le nombre d’objets, plutôt que sur le nombre d’usines exploitant la ressource. Ainsi, les recettes du Chevalet de pompage et de la Pompe côtière sont simplifiées en une recette dont le coût est plus élevé et qui ne produit qu’un objet par seconde. Une fois que nous avons calculé une quantité de Pétrole brut et d’ Eau pour la solution, il est trivial de reconvertir ce nombre de production en un nombre d’usines.
|
|
|
|
|
Sort | |
|---|---|---|---|---|---|---|
|
1 | 0 | -20 | 0 | 0 | 0 |
|
0 | 1 | -10 | -15 | -15 | 0 |
|
0 | 0 | 5 | -20 | 0 | -5 |
|
0 | 0 | 9 | 15 | -15 | 0 |
|
0 | 0 | 11 | 0 | 10 | -100 |
| Coût | 1000 | 100 | 1 | 1 | 1 | 0 |
Problème dual de minimisation
Le problème de ce programme linéaire est que nous voulons minimiser le coût de notre solution, alors que l’algorithme du simplexe est conçu pour maximiser un objectif. Heureusement, il existe un moyen simple de convertir un problème de minimisation en un problème de maximisation qui peut lui être résolu à l’aide de l’algorithme du simplexe. Pour ce faire, on convertit le problème de minimisation en son “problème dual de maximisation”. Une fois qu’un problème de minimisation est converti en son problème dual de maximisation, il est possible de résoudre le problème dual à l’aide de l’algorithme du simplexe. La solution à la maximisation du problème dual est la même que la solution à la minimisation du problème original, nous pouvons donc l’accepter comme notre solution.
Le problème dual est simplement une transposition du problème original, ou une permutation des lignes et des colonnes. On obtient ainsi :
|
|
|
|
|
Coût | |
|---|---|---|---|---|---|---|
|
1 | 0 | 0 | 0 | 0 | 1000 |
|
0 | 1 | 0 | 0 | 0 | 100 |
|
-20 | -10 | 5 | 9 | 11 | 1 |
|
0 | -15 | -20 | 15 | 0 | 1 |
|
0 | -15 | 0 | -15 | 10 | 1 |
| Sort | 0 | 0 | -5 | 0 | -100 | 0 |
Afin de traiter les valeurs excédentaires potentielles, la programmation linéaire ajoute généralement des variables ’excédentaires’ ou ‘souples’ au programme. Par exemple, pour qu’une usine ne produise que du Pétrole lourd, il n’existe aucune solution qui n’implique pas une certaine quantité excédentaire de Pétrole léger et de Gaz de pétrole. Ces variables sont représentées par des colonnes supplémentaires dans la matrice où chaque colonne a une valeur ‘1’ dans la ligne correspondant à son objet.
|
|
|
|
|
+
|
+
|
+
|
+
|
|
Coût | |
|---|---|---|---|---|---|---|---|---|---|---|---|
|
1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1000 |
|
0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 100 |
|
-20 | -10 | 5 | 9 | 11 | 0 | 0 | 1 | 0 | 0 | 1 |
|
0 | -15 | -20 | 15 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
|
0 | -15 | 0 | -15 | 10 | 0 | 0 | 0 | 0 | 1 | 1 |
| Sort | 0 | 0 | -5 | 0 | -100 | 0 | 0 | 0 | 0 | 0 | 0 |
Maintenant, nous avons enfin une matrice canonique qui peut être résolue à l’aide de l’algorithme du simplexe.
Résolution avec le simplexe
Le but final de l’algorithme du simplexe est d’arriver à une matrice où la fonction objectif (dans ce cas, la dernière ligne de la matrice) ne contient aucun nombre négatif. Dans notre matrice initiale, notez que notre ligne d’objectif comporte deux colonnes avec des valeurs négatives, représentant les deux objets que nous voulons produire. Afin d’atteindre notre solution, nous devons simplement appliquer des opérations de ‘pivot’ jusqu’à ce que notre ligne d’objectif n’ait plus de valeurs négatives.
Pivot n°1
Une opération de pivot simplexe comporte quatre étapes.
- Choisissez une colonne à faire pivoter. Il doit s’agir d’une colonne négative, et on la choisit généralement comme le plus grand nombre négatif. Dans notre matrice, il s’agirait de la colonne Gaz de pétrole.
- Choisissez une ligne à faire pivoter. Vérifiez chaque ligne où la colonne choisie a une valeur supérieure à zéro, et calculez le rapport entre la colonne de coût de cette ligne et la valeur de la colonne choisie de cette ligne. La ligne pivot est celle dont le rapport est le plus faible. Dans notre matrice, nous pouvons vérifier chaque ligne :
-
: la colonne est à 0, ignorez cette ligne.
-
: la colonne est à 0, ignorez cette ligne.
-
: la colonne est à 11, la colonne de coût est à 1, le rapport est donc de 1/11.
-
: la colonne est à 0, ignorez cette ligne.
-
: la colonne est à 10, la colonne de coût est à 1, le rapport est donc de 1/10.
- Le rapport le plus faible est pour la ligne , avec 1/11, nous allons donc faire pivoter cette ligne.
-
- Divisez la ligne pivot par la réciproque de l’objet pivot. Dans notre ligne pivot, cela donne -20/11, -10/11, 5/11, 9/11, 1, 0, 0, 1/11, 0, 0, 1/11
- Ajoutez des multiples de la ligne pivot aux autres lignes pour changer la colonne pivot en 0. Le résultat final est le suivant :
| +
|
+
|
+
|
+
|
+
|
|
|
|
|
|
Coût |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1000 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 100 |
| -1 9/11 | -10/11 | 5/11 | 9/11 | 1 | 0 | 0 | 1/11 | 0 | 0 | 1/11 |
| 0 | -15 | -20 | 15 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 18 2/11 | -5 10/11 | -4 6/11 | -23 2/11 | 0 | 0 | 0 | -10/11 | 0 | 1 | 1/11 |
| -181 + 9/11 | -90 10/11 | 40 5/11 | 81 9/11 | 0 | 0 | 0 | 9 1/11 | 0 | 0 | 9 1/11 |
Maintenant, continuons avec le pivot suivant.
Pivot n°2
Colonne 1 (-181 9/11), Ligne 5 (rapport : 1/200)
| +
|
+
|
+
|
+
|
+
|
|
|
|
|
|
Coût |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 13/40 | 1/4 | 1 + 11/40 | 0 | 1 | 0 | 1/20 | 0 | -11/200 | 9999 + 199/200 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 100 |
| 0 | -1 1/2 | 0 | -1 1/2 | 1 | 0 | 0 | 0 | 0 | 1/10 | 1/10 |
| 0 | -15 | -20 | 15 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 1 | -13/40 | -1/4 | -1 11/40 | 0 | 0 | 0 | -1/20 | 0 | 11/200 | 1/200 |
| 0 | -150 | -5 | -150 | 0 | 0 | 0 | 0 | 0 | 10 | 10 |
Pivot n°3
Colonne 2 (-150), Ligne 2 (rapport : 100)
| +
|
+
|
+
|
+
|
+
|
|
|
|
|
|
Coût |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1/4 | 1 + 11/40 | 0 | 1 | -13/40 | 1/20 | 0 | -11/200 | 9967 + 99/200 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 100 |
| 0 | 0 | 0 | -1 1/2 | 1 | 0 | 1 1/2 | 0 | 0 | 1/10 | 150 + 1/10 |
| 0 | 0 | -20 | 15 | 0 | 0 | 15 | 0 | 1 | 0 | 1501 |
| 1 | 0 | -1/4 | -1 11/40 | 0 | 0 | 13/40 | -1/20 | 0 | 11/200 | 32 + 101/200 |
| 0 | 0 | -5 | -150 | 0 | 0 | 150 | 0 | 0 | 10 | 15010 |
Pivot n°4
Colonne 4 (-150), Ligne 4 (rapport : 133 2/5)
| +
|
+
|
+
|
+
|
+
|
|
|
|
|
|
Coût |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 19/20 | 0 | 0 | 1 | -1 3/5 | 1/20 | -17/200 | -11/200 | 9839 91/100 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 100 |
| 0 | 0 | -2 | 0 | 1 | 0 | 3 | 0 | 1/10 | 1/10 | 300 + 1/5 |
| 0 | 0 | -1 1/3 | 1 | 0 | 0 | 1 | 0 | 1/15 | 0 | 100 1/15 |
| 1 | 0 | -1 19/20 | 0 | 0 | 0 | 1 3/5 | -1/20 | 17/200 | 11/200 | 160 9/100 |
| 0 | 0 | -205 | 0 | 0 | 0 | 300 | 0 | 10 | 10 | 30020 |
Pivot n°5
Colonne 3 (-205), Ligne 1 (rapport : 5046 7/65)
| +
|
+
|
+
|
+
|
+
|
|
|
|
|
|
Coût |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 20/39 | -32/39 | 1/39 | -17/390 | -11/390 | 5046 7/65 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 100 |
| 0 | 0 | 0 | 0 | 1 | 1 1/39 | 1 14/39 | 2/39 | 1/78 | 17/390 | 10392 27/65 |
| 0 | 0 | 0 | 1 | 0 | 80/117 | -11/117 | 4/117 | 1/117 | -22/585 | 6828 41/195 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1000 |
| 0 | 0 | 0 | 0 | 0 | 105 5/39 | 131 31/39 | 5 10/39 | 1 5/78 | 4 17/78 | 1064472 1/13 |
La dernière ligne de la matrice n’a maintenant aucune valeur négative, elle est donc considérée comme la solution. La solution peut être trouvée à partir de la dernière ligne, où les cinq premières colonnes représentent les valeurs excédentaires (dans ce cas, toutes nulles), les deux valeurs suivantes représentent les entrées Pétrole brut et Eau, les trois valeurs suivantes représentent le nombre d’usines qui produisent le Raffinage avancé, le Craquage du pétrole lourd, et le Craquage du pétrole léger, et la dernière valeur représente le ‘coût’ de cette solution.
Ainsi, notre solution nécessite 105 5/39 , 131 31/39 , 5 10/39 , 1 5/78 
, and 4 17/78 .
Cette solution peut être comparée au résultat dans FactorioLab.
Onglet Matrice
L’onglet Matrice de FactorioLab, une fonctionnalité relativement nouvelle, vous permet de jeter un coup d’œil sous le capot du résolveur simplexe. Pour les chaînes de recettes qui peuvent être résolues sans, cet onglet est pratiquement vide, mais lorsque le simplexe est utilisé, l’onglet dévoile de nombreux détails et vous permet même de personnaliser la fonction de coût utilisée par le résolveur.
Informations sur les résultats
Le premier tableau expose les détails sur les résultats du résolveur simplexe.
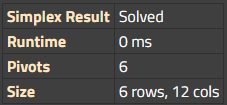
- Le Résultat du simplexe du résolveur
- Skipped : Le résolveur simplexe n’a pas été utilisé, soit parce qu’il est désactivé, soit parce qu’il n’était pas nécessaire pour résoudre la chaîne de recettes.
- Failed : Le résolveur simplexe a rencontré une erreur, généralement due à une boucle de recette qui ne peut être résolue (par exemple, si les plaques de fer nécessitent deux engrenages et que les engrenages nécessitent deux plaques de fer).
- Cancelled : L’utilisateur a annulé le résolveur manuellement lorsqu’il y a été invité après avoir fonctionné pendant au moins cinq secondes.
- Solved : Une solution valide a été trouvée.
- La Durée d’exécution du résolveur simplexe, en ms.
- Le nombre total de Pivots effectués par le résolveur.
- La Taille de la matrice canonique
Modificateurs de coûts
Le deuxième tableau permet à l’utilisateur de modifier la fonction de coût utilisée dans la matrice canonique.
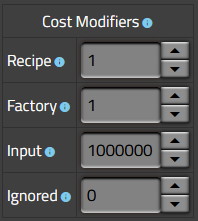
- Recipe est un facteur qui multiplie le coût des recettes ayant un coût défini, généralement des recettes minières représentant des ressources brutes
- Factory est un facteur qui multiplie le coût du nombre d’usines elles-mêmes, qui n’est généralement qu’une considération secondaire.
- Input définit le coût des objets qui ne peuvent être produits par aucune recette, comme le Bois dans Factorio
- Ignored définit le coût des objets qui ont été explicitement ignorés, qui est égal à zéro par défaut.
Tableau canonique simplexe et solution
Le troisième tableau montre à la fois la matrice canonique générée par le calculateur et la ligne de solution avec le coût final. Notez qu’il s’agit d’un problème dual de minimisation, ce qui correspond à la façon dont le calculateur minimise le coût en utilisant la méthode du simplexe. Dans chaque ligne de recette, le coût de la recette est affiché et peut également être modifié à l’aide du champ de saisie du coût situé à droite. Les valeurs sont représentées en objets/seconde dans ce tableau, quelle que soit la sélection du taux d’affichage de l’utilisateur, car c’est ainsi que les calculs sont toujours effectués en interne.
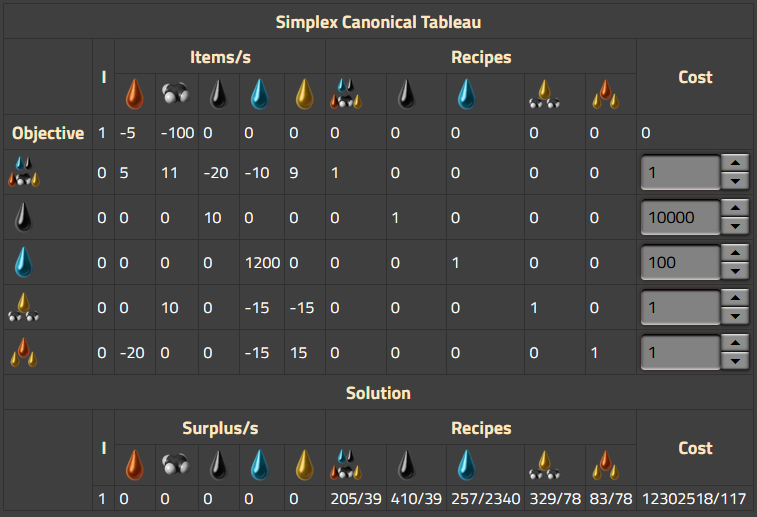
Algorithmes alternatifs
L’algorithme du simplexe utilisant la maximisation duale s’est avéré être une méthode très efficace pour résoudre les calculs d’usine. Cependant, le simplexe n’est pas le seul algorithme permettant de résoudre un programme linéaire. Il existe d’autres méthodes telles que le simplexe révisé, l’algorithme criss-cross, la méthode de l’ellipsoïde, l’algorithme de Karmarkar, et la méthodes de points intérieurs. En fait, en 2019 seulement, le temps d’exécution a été amélioré par un nouvel algorithme de temps de multiplication de matrice. Au fur et à mesure que le programme linéaire prend de l’ampleur, en particulier dans les parties de Factorio modées, l’algorithme du simplexe utilisé par FactorioLab peut prendre beaucoup de temps pour trouver une solution, surtout lorsque les mods introduisent des recettes de ‘recyclage’ qui introduisent un grand nombre de boucles. Avec des recherches plus poussées, il est possible qu’un meilleur algorithme pour résoudre les programmes linéaires des usines puisse être développé.
Résumé rapide
- Les usines simples sont faciles à calculer à la main, lorsque les objets ne sont produits que par une seule recette.
- Lorsque des objets sont produits par plusieurs recettes différentes, il faut trouver un moyen de déterminer la quantité de chaque recette qui doit être utilisée.
- Comme il existe de multiples solutions potentielles, nous devons mesurer le coût d’une solution pour déterminer la meilleure.
- Le simplexe est l’algorithme le plus couramment utilisé (bien qu’il ne soit pas le plus rapide) pour résoudre ce type de problèmes, tant dans la communauté Factorio que dans celle des mathématiques.
-
FactorioLab utilise l’algorithme du simplexe pour trouver la solution optimale pour les usines complexes et permet aux utilisateurs de :
- Personnaliser la fonction de coût, car elle est subjective.
- Utiliser des ensembles de données de mods courants.
- Effectuer des calculs et planifier des usines à partir d’appareils mobiles ou au travail
- Calculer la quantité de carburant pour fusée que vous pouvez produire à partir d’une seule raffinerie.
Rejoignez le Discord de FactorioLab pour en apprendre davantage !
Contribuer
Comme toujours, nous attendons vos contributions pour les Alt-F4, que cela soit par la soumission d’un article ou en aidant pour les traductions. Si vous avez quelque chose d’intéressant en tête que vous souhaitez partager avec la communauté, vous êtes au bon endroit. Si vous n’êtes pas sûr, nous serons heureux de vous aider en discutant structure, contenu et idées. Donc si vous voulez vous impliquer dans les Alt-F4, rejoignez-le Discord pour ne rien rater !