Alt-F4 #11 - Curiosità Scientifiche 30-10-2020
tradotto da Frank_si_narra

Tabella dei Contenuti
-
Un esame scientifico del mondo di Factorio
pocarski - Nauvis è una nana bianca
- Parliamo delle meccaniche orbitali di Nauvis
- Nauvis riflette almeno l’88,3% di tutta la luce che lo colpisce
- Le testate nucleari sono decisamente meno potenti del dovuto
- Il combustibile nucleare è 3 volte più caldo della superficie solare
- Gli oggetti hanno densità incredibilmente basse
-
Archivi di Nauvis: Techniche Antiquate
stringweasel - Come contribuire
Benvenuti nell’undicesima edizione di Alt-F4, in cui si parla sia di analisi matematica che di storia. Quindi, sull’attenti, scolari! Pocarski si è preso la briga di controllare se la matematica reale funzionasse anche su Nauvis. Allarme spoiler: no. In oltre stringweasel torna un’altra volta per guardare la storia, più precisamente sulle meccaniche del passato ora obsolete.
Un esame scientifico del mondo di Factorio pocarski
La sospensione dell’incredulità è un concetto ben noto, che non ferma alcuni di noi dall’ignorarlo completamente. Recentemente mi sono imbattuto in un post su Reddit in cui veniva calcolata la densità di Nauvis, e questo mi ha dato l’idea di fare una lista giusto per divertimento di tutte le ridicole imprecisioni scientifiche dell’universo di Factorio. In fondo, questa comunity è sempre stata composta da un mucchio di nerd con troppo tempo libero, quindi perché non indulgiare un po’ in cose ricreative per nerd?
Avviso scontato: questo articolo conterrà un’eccessiva quantità di matematica; se avete una grave intolleranza matematica, sentitevi liberi di saltarlo.
Nauvis è una nana bianca
Questa è una rivisitazione del post di u/DaveMcW di cui prima. Notare che questa teoria assuma che il ciclo notte/giorno del pianeta sia dovuto alla sua rotazione, cosa che più avanti metterò in discussione.
I grandi corpi celesti sono tenuti assieme dall’attrazione gravitazionale, perché un pianeta non si smembri a causa della forza centrifuga, la gravità all’equatore deve essere più grande della forza centripeta. Assumendo che il pianeta sia sferico, e usando le equazioni per la forza centripeta e quella gravitazionale, possiamo dimostrare che:
$ \frac{GMm}{r^2} > mr\omega^2 $, dove $G$ è la costante di gravitazione universale, $r$ è il raggio planetario, $M$ è la massa del pianeta, $\omega$ è la velocità angolare del pianeta,e $m$ è la massa dell’oggetto su cui le forze agiscono;
$ \frac{GM}{r^2} > r\omega^2 \quad\Rightarrow\quad GM > r^3\omega^2 $
$ \frac{4}{3}\pi r^3 = V \quad\Rightarrow\quad r^3 = \frac{3V}{4\pi} $, dove $V$ è il volume del pianeta;
$ GM > \frac{3V\omega^2}{4\pi} \quad\Rightarrow\quad G\frac{M}{V} > \frac{3\omega^2}{4\pi} $
$ \omega = \frac{2\pi}{T} \quad\Rightarrow\quad \frac{3\omega^2}{4\pi} = \frac{3\pi}{T^2};\quad \frac{M}{V} = \rho $, dove $ \rho $ è la densità del pianeta;
$ \frac{G\rho}{3} > \frac{\pi}{T^2} \quad\Rightarrow\quad \rho > \frac{3\pi}{GT^2} $
Finiamo con l’avere un’espressione della densità solo con il periodo rotazionale. Immettendo i valori di $ \pi $ e $G$, oltre al periodo notte/giorno di Factorio (T = 25,000 ticks = 416.(6) secondi) troviamo che:
$ \rho > 813,400 \mathrm{kg/m^3} $
La densità di Nauvis deve essere quindi maggiore di 813,400 kg/m3. Per darvi un’idea, la densità dell’acciaio è di 8,050 kg/m3, quella del piombo 11,350 kg/m3, mentre l’osmio metallico, il materiale più denso sulla terra, arriva a 22,570 kg/m3. 813,400 kg/m3 è un numero così estremo che Nauvis dovrebbe essere una nana bianca per avere questa densità. Una nana bianca è ciò che rimane dopo il collasso di una stella di piccole dimensioni, che lascia un residuo delle dimensioni della Terra. La superficie delle nane bianche ha una temperatura che può variare da 8.000 K a 40.000 K. Il sole ha una temperatura superficiale di poco inferiore ai 6.000 K. Il suolo di Nauvis deve essere un ottimo isolante termico!
Parliamo delle meccaniche orbitali di Nauvis
Siccome tutte le ombre sul suolo non cambiano di lunghezza o direzione durante l’arco della giornata dobbiamo concludere che la fonte luminosa non cambia posizione nel cielo, quindi Nauvis è rotazione sincrona con la sua stella. Ne consegue che il ciclo notte/giorno che osserviamo, sia dovuto a qualche oggetto che occlude la luce. Basandosi sulla frequeza delle notti, l’oggetto è probabilmente in orbita attorno al pianeta, ma non si può trattare di una luna perché un corpo così massiccio vicino a Nauvis lo farebbe mettere in rotazione sincrona con esso. Quindi la notte deve essere causata da una nube di oggetti in orbita attorno al pianeta — il che spiegherebbe anche lo schianto dell’ingegnere: ha impattato delle roccie in orbita.
Una spiegazione alternativa per il ciclo notte/giorno, proposta da alcuni, è che la stella parente di Nauvis sia una cefeide variabile, un tipo di stella che varia in dimensioni, temperatura e luminosità con un ritmo regolare. Personalmente penso che sia impossibile poiché la variazione di luminosità è troppo ampia, specialmente per avvenire in un tempo così breve.
Nauvis riflette almeno l’88,3% di tutta la luce che lo colpisce
Un semplice solar panel di Factorio ha un’area di 9 m2 e produce 60 kW durante il giorno. Da questi numeri troviamo che la superficie del pianeta viene irradiata per almeno 6,(6) kW/m2 (contro i 1 kW/m2 sulla della Terra). Considerando che la temperatura ambientale media su Nauvis è pari a 15 °C e che è in rotazione sincrona, possiamo usare una versione leggermente modificata della formula per la temperatura efficace:
$ T = \root{4}\of{\frac{1}{2}\frac{P(1-a)}{\sigma}} $, dove $P$ rappresenta l’energia ricevuta per unità di superficie, $T$ è la temperatura assoluta della superficie, $a$ è l’albedo (la nostra incognita) e $\sigma$ è la costante di Stefan-Boltzmann;
$ a = 1 - \frac{2\sigma T^4}{P} $
$ T = 15\mathrm{°C} = 288.15\mathrm{K} $
$ P = 6666.(6)\mathrm{W/m^2} $
$ a = 0.8827 $
Nauvis deve avere un albedo di almeno 0,883 per mantenersi a 15 °C. Ciò significa che riflette almeno l’88,3% della luce che lo colpisce. Siccome l’efficienza del nostro pannello solare è probabilmente minore del 100%, e Nauvis probabilmente non è un perfetto corpo nero, l’albedo è sicuramente anche maggiore.
Per offrire un riferimento, la Luna ha un’albedo di 0,14 e la Terra di 0,306. Se la Luna avesse un albedo di 0,883, sarebbe 6,3 volte più luminosa. Se fosse invece la terra ad avere una albedo di 0,883, avrebbe una temperatura superficiale media di -88,5 °C.
Le testate nucleari sono decisamente meno potenti del dovuto
È giunto il momento di ritornare dallo spazioe e didicarci a creazioni artificiali. Un pezzo di Uranio-235 su Factorio produce 10 celle di combustibile, ciascuna delle quali contiene 8 GJ (ignoriamo per un attimo il bonus vicinanza). Questo vuol dire che un singolo pezzo di U-235 ha 80 GJ di energia di fissione al suo interno, e siccome una testata nucleare richiede 30 pezzi di U-235, con il 20% di efficienza di fissione (che è quello che si ottiene con la ricerca di fissione avanzata; un passo richiesto per anche la più piccola testata), dovrebbe avere un potenziale esplosivo di 115 tonnellate di TNT. Potrebbe non suonare un numero così elevato, ma solo lo sprite dell’esplosione si estenderebbe per 60 tiles. Una bomba del genere distruggerebbe completamente tutto ciò che si trova nel raggio di 100 tiles, ucciderebbe qualsiasi essere vivente in un raggio di 250 tiles, e creerebbe danni in un raggio di 500 tiles (basandosi su Nukemap).
Per fare un paragone, la testata nucleare in-game dannegia solo in un raggio inferiore a 40 tiles, 12,5 volte meno.
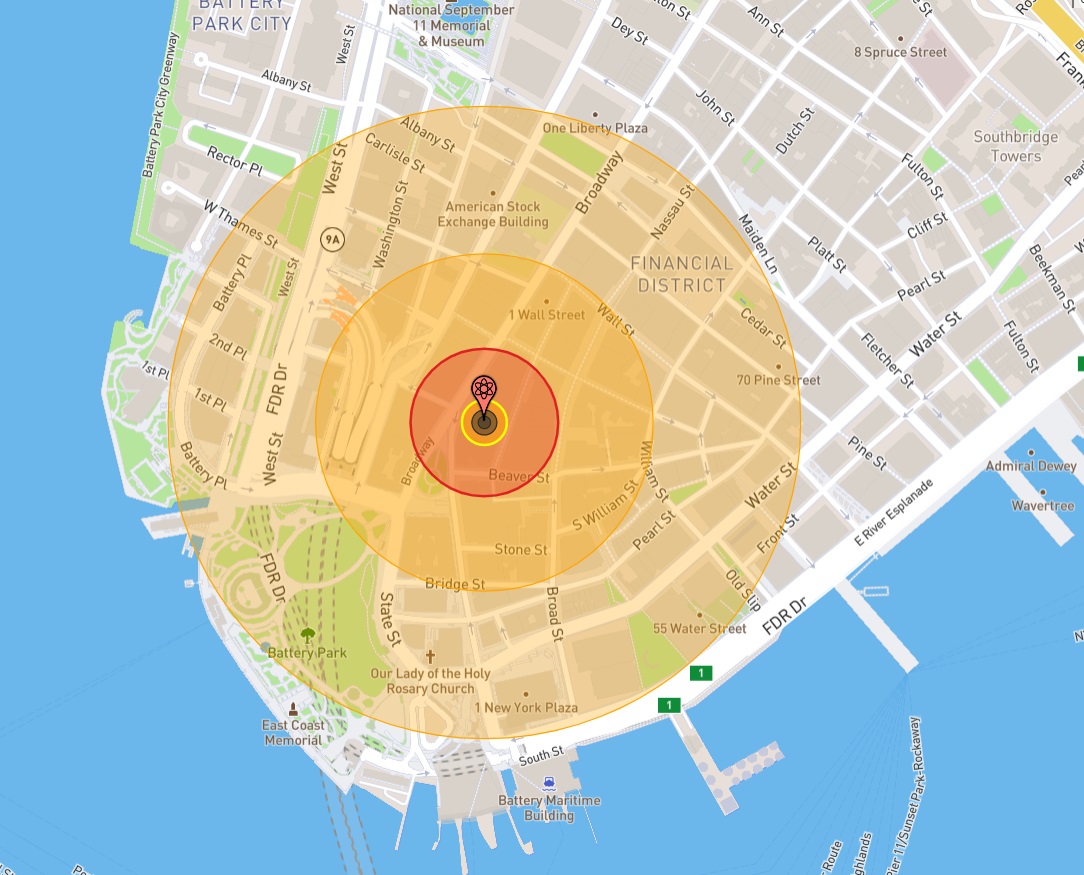
Gli anelli del diagramma denotano, in ordine crescente:
- Il cratere e i bordi del cratere (sprite della terra bruciata)
- Palla di fuoco (Sprite dell’esplosione)
- Grave danno strutturale (la zona di “annichilimento totale”)
- Probabilità del 100% di ustione di terzo grado (la zona di “sterminazione totale”)
- Posssibilità del 50% di ustioni di primo grado (la zona di “danneggiamento”)
In tutta onestà, se consideriamo che al contributo energetico totale partecipa anche l’U-238 otteniamo un’esplosione leggermente minore. Rimane comunque ridicolo, solo poco di meno.
E a proposito di energia nucleare…
Il combustibile nucleare è 3 volte più caldo della superficie solare
Le locomotive hanno un consumo costante di energia pari a 600 kW, ma un carburante migliore le rende più veloci. Ciò significa che un carburante di qualità superiore ne incrementa l’efficienza.
Possiamo esprimere l’output di energia in funzione di accelerazione e velocità:
$ P_u = \frac{dA}{dt} = \frac{Fds}{dt} = Fv = mav $, dove $P_u$ è l’output efficace, $m$ è la massa del treno, $a$ è la sua accelerazione e $v$ la sua velocità massima.
Ponendo l’efficienza $N$:
$ N = \frac{P_u}{P_c} = \frac{mav}{P_c} $, dove $P_c$ è l’energia totale consumata (600 kW);
$ \frac{N_1}{N_0} = \frac{a_1v_1}{a_0v_0} $, dove $N_0$, $a_0$, e $v_0$ sono rispettivamente l’efficienza, l’accelerazione e la velocità massima alimentando il mezzo a carbone; $N_1$, $a_1$, e $v_1$ sono gli stessi parametri con un carburante qualsiasi.
Quindi l’efficienza del carburante divisa per quella del carbone è esattamente uguale alla nuova velocità massima per la nuova accelerazione, vuol dire che il carburante nucleare è $1.15 \times 2.5 = 2.875$ volte più efficiente del carbone. Dato che le locomotive possono usare qualsiasi carburante, è giusto affermare che usino una macchina termica. Se questo motore lavora con la massima resa possibile (calcolata secondo il [ciclo di Carnot]https://it.wikipedia.org/wiki/Ciclo_di_Carnot), essa è:
$ N = 1 - \frac{T_{c}}{T_{h}} $, dove $T_c$ è la temperatura assoluta della parte fredda del motore (288,15 K; temperatura ambiente), e $T_h$ è la temperatura assoluta della parte calda del motore (scaldata dal carburante). È ragionevole assumere che il carbone di Nauvis bruci a 165 °C (438,15 K), basandosi sulla temperatura del gas proveniente daun boiler. Questo vuol dire che l’efficienza di un treno alimentato a carbone è:
$ N = 1 - \frac{288.15\mathrm{K}}{438.15\mathrm{K}} = 0.34 $
L’efficienza del carburante nucleare è 2,875 volte maggiore (guarda sù) ovvero 0,98. Ciò significa che:
$ 1 - \frac{288.15\mathrm{K}}{T} = 0.98 $
$ T = \frac{288.15\mathrm{K}}{1-0.98} = 18297.525\mathrm{K} = 18024.375\mathrm{°C} $
Il carburante nucleare ha una temperatura superiore a 18.000 °C. Piccola curiosità, se la temperatura del vapore proveniente da un boiler fosse solo di 3,68 gradi superiore, l’efficienza del carburante nucleare sarebbe esattamente 1. E se fosse anche poco più di 168,68 °C, le leggi della fisica smetterebbero di funzionare.
Ma non preoccupatevi, non sarebbe un grosso problema perché sono già largamente infrante senza violare la termodinamica. Per esempio…
Gli oggetti hanno densità incredibilmente basse
Questa parte è basata sul post di u/Maouitippitytappin su Reddit riguardo il suo viaggio alla ricerca di una scala per riferimento su Factorio. Riassumendo il suo lavoro: basandosi sul consumo di una fornace base per raffinare una piastra di ferro possiamo trovare la massa di una singola piastra, che dai calcoli risulta essere 40 grammi. Con lo stesso calcolo una piastra di rame dovrebbe pesare 65 grammi. (le fonti variano; si potrebbero ottenere risultati differenti)
Con questi dati otteniamo che la massa di materiali utilizzati per la costruzione di una locomotiva è pari a 14,6 kg. Poiché la locomotiva ha un volume di 24 m3 (assumendo che l’altezza sia 2 metri basandosi sull’aspetto) ha una densità di 0,6 kg/m3, ovvero la metà di quella dell’aria. Ciò significa che le locomotive possono essere usate come palloncini!

Forse Nauvis davvero è in rotazione, e lo fa così velocemente perché il galleggiamento a causa della forza centrifuga agisca verso il basso sugli oggetti. Questo fornirebbe una buona spiegazione del perché si possano far entrare 240 locomotive in una cesta di 1 m3; perché probabilmente si possono accartocciare. Una cosa che però non riuscirebbe a spiegare, è il fatto che i treni possano girare a 300 km/h in una curva di 12 metri senza deragliare. Dovrebbero subire 60 g di accelerazione andando alla velocità massima:
$ a = \frac{v^2}{r} = \frac{(82.8\mathrm{m/s})^2}{12\mathrm{m}} = 571.32\mathrm{m/s^2} = 58.26g $
Siccome le rotaie sono palesemente in piano, i treni devono avere ruote come quelle sui vagoni delle montagne russe, che tengono il tracciato su 3 lati. Personalmente adoro l’idea di treni palloncino che sfrecciano a 300 km/h con un motore a 18.000 °C, ma forse sono l’unico.
Archivi di Nauvis: Techniche Antiquate stringweasel
Nel corso degli anni Factorio è cambiato molto. Nuovi giocatori, nuove meccaniche, nuovi sviluppatori, nuove strategie, etc. E quando cambiano i tempi, alcune tecniche di gioco vengono lasciate indietro per fare strade a nuovi e migliorati metodi. Come tempo fa Kerbals atterravano su Mun solo usando ali come mezzo di discesa, o i giocatori di Minecraft piazzavano dei minecart boosters per proppellere i loro carrelli. Ci sono vecchi rituali e tecniche che non usiamo più nell’era moderna. Trovo sempre interessante guardare al passato per vedere cosa si faceva una volta, ed è esattamente ciò che faremo qui.
Pali della Vittoria
Prima della 0.13, i biter erano estremamente spaventati da qualsiasi struttura che costruivi. Non provavano neanche ad espandersi vicino a qualsiasi cosa piazzata dal subdolo giocatore. Questo è risultato nella nascita nella community di un’usanza: piazzare pali della vittoria. Potevi piazzare una qualsiasi entità, solitamente qualcosa di economico tipo una cesta di legno o un palo dell’elettricità e potevi tenerti la tua terra giustamente guadagnata. C’è un bellissimo video di NegativeRoot che spiega il rituale. Ironicamente, dopo la 0.13, quando i biter non erano più spaventati dalle nostre strutture, alcuni ignari giocatori trovarono nidi di biter all’interno delle loro basi indifese!

Perdita di compressione nelle curve
Molti non ci pensano, ma i nastri trasportatori sono le entità più complesse del gioco. Ora “funziona e basta”, ma ci sono voluti anni per limare tutti i bug e mal di testa che provocava. Roba tipo gli oggetti che si incastrano, gli inserter che non prendevano l’ultimo oggetto sul nastro, e essere obbligati ad usare i sottopassaggi per aumentare gli UPS. Ancora più infame, ma da lungo tempo dimenticato, è la perdita di compressione nelle curve pre-0.12 e le tecniche utilizzate per mantenere la portata al 100%.
All’epoca, i nastri perdevano la compressione attorno alle curve a causa di come le collisioni venivano gestite. Una volta gli oggetti venivano considerati entità singole con bordi di collisione a se stanti che causavano l’involontario scontro degli oggetti nelle curve; oggi questi oggetti non hanno affatto bordi di collisione. Persino una volta i giocatori volevano fare le cose in grande ovviamente, ed erano quindi costretti ad aggirare la perdita di compressione. Per costruzioni più piccole, una compressione del ~100% era possibile rimpiazzando le curve con nastri di livello superiore o usando due splitter. Ma in fabbriche più grandi con larghi bus — dove i nastri sono già tutti al livello massimo — era necessario avvaleresi di tecniche più complesse. Tipicamente, questi design erano ideati del leggendario belt wizard MadZuri, per essere utilizzati nelle immense fabbriche di ColonelWill.
Lunghi dibattiti sono scaturiti attorno a quale dovrebbe essere il comportamento degli oggetti sui nastri nelle curve, anche dopo che la perdita di compressione venne risolta nella 0.12. Dovrebbero muoversi ad una velocità costante e quindi quelli sulla corsia interna uscirebbero prima, come succede ora? O la linea interna si dovrebbe muovere più lentamente in modo tale da essere sincrona con quella esterna? Essenzialmente la discussione era realismo vs gameplay, e a volte inconsapevolmente, latenza vs portata. Ad alcuni piacevano semplicemente tutti i video che venivano postati sulle linee di produzione nelle curve nel mondo reale.
La meccanica dei nastri trasportatori è una di quelle cose che, se non sono perfette, tutti notano che qualcosa non quadra. Ma appena funzionano, passano inosservate per la loro intuitività e semplicità. Questo è perché le belle implementazioni devono sembrare intuitive e nascondere l’enorme complessità che vi è dietro con una semplice interfaccia. E come ben sapete, gli ingegneri di oggi non commentano mai sulle meccaniche dei nastri trasportatori. Essi sono semplici da usare e hanno senso. Il che vuol dire che il team di Factorio ha davvero fatto un capolavoro nell’implementazione di questa meccanica.
Splitter con priorità manuali
Gli splitter hanno acquisito la capacità di priorizzare l’imput da destra/sinistra nella 0.16.17 (insieme all’introduzione dei filtri). In precedenza, gli splitter con priorità dovevano essere costruiti con ingegno, spaghetti e molti circuiti. Questo portò nel 2016 ad un periodo in cui questi design erano al centro dell’attenzione. Giocatori come Steejo, raspi, canidae, e Captain Konzept, per nominarne alcuni, iniziarono rapidamente approfondite ricerche e test “per il bene della fabbrica”.

Costruire uno splitter a priorità usando solo i circuiti logini non era impresa da poco, soprattutto allora, ma questo non fermò la nostra community specialistica; sormontarono vari ostacoli vigorosamente. Per esempio, quando si leggeva un nastro alla capienza massima, potevano comparire 6 o 7 oggetti in modo apparentemente casuale. Ancora peggio, non c’è alcun modo di differenziare un nastro alla massima portata da uno terminale. In entrambi i casi, il circuito logico leggeva comunque 8 (oppure 6!) oggetti presenti. Questo portò a vari design complicati, ciascuno con i propri metodi e tecniche magistralmente implementate per farli funzionare. Captain Konzept realizzò un magnifico video spiegando i vari approcci dei diversi giocatori (e un altro ancora più tardi in cui li metteva a confronto con i nuovi splitter a impostazione interna della priorità).
Dopo un po’, le persone realizzarono che, nella maggiorparte dei casi, un design complesso per gli splitter a priorità non fosse davvero necessario, e il bilanciamento introdotto dagli sviluppatori era tranquillamente sufficiente. Questa linea di pensiero cambiò di nuovo in seguito all’aggiunta nella 0.16.17 degli splitter migliorati. Ad ogni modo, il punto è che siano riusciti a creare uno splitter a priorità manuale! Tutavia questa non è l’unica cosa folle che gli esperti riuscirono a costruire usando le meccaniche dei semplici splitter.
Magia nera: Splitter a filtraggio meccanico
Come detto prima, gli splitter pre-0.16.17 (o 0.16.16) si comportavano diversamente e non avevano impostazioni per il filtraggio. Questo non ha però comunque impedito alla community di abusare degli splitter per filtrare gli oggetti — questa volta senza l’utilizzo dei circuiti! La cosa è iniziata con questo post in cui SPolygon diceva che il suo splitter non divideva la roba correttamente. Come daniel34 ha spiegato, lo splitter non sceglie dove mettere l’oggetto solo in base a dove ha messo quello di prima, ma anche in base al tipo di oggetto. Questo attirò l’attenzione del leggendario XKnight che immediatamente fece uscire dei modelli che abusavano di questa meccanica. Qusti design sembravano rasentare la magia e lasciarono senza parole anche gli sviluppatori! All’incirca un anno dopo, u/tzwaan riportò alla luce il lavoro di XKnight, continuò la ricerca per poi mostrarla al mondo di Reddit, dandogli il nome di “smista oggetti a magia nera”
È necessario tenere a mente che questi splitter non hanno alcuna capacità filtrante voluta. Eppure, gli esperti della community sono riusciti ad ottenere il filtraggio abusando delle loro meccaniche intrinseche. Allora, nel 2016/2017, la maggiorparte della community era ossessionata dagli splitter — e lo splitting in base a priorità e il folle filtraggio a magia nera. Al posto di lamentarsi con gli sviluppatori perché introducessero queste meccaniche internamente al gioco, si misero a lavoro per risolvere queste magagne comuni semplicemente giocando al gioco. A mio parere questa è una testimonianza di quanto si magnifica la community di Factorio e del livello di talento e dedicazione di alcuni dei più appassionati giocatori.
Come contribuire
Come sempre, siamo in cerca di persone che abbiano voglia di partecipare alla creazione degli articoli di Alt-F4, che sia scrivendo in prima persona uno di essi o anche solo aiutando con la traduzione dei precedenti. Se hai qualcosa di interessante da raccontare alla comunity in modo ordinato, questo è il posto per farlo. Se sei insicuro su qualcosa, saremo grati di aiutarti discutendo di concetti e interrogandoci sulla struttura testuale. Se la cosa ti va a genio, entra nel server Discord per iniziare!