Alt-F4 #27 - Designing the Unnecessary 12-03-2021

This week, pocarski continues his descent into belt-related madness by taking a look at universal balancers. The result is as crazy as it is useless, so you know we’re in for a treat!
Universal 8-8: Perfectly Balanced, as All Things Should Be pocarski
Recently, I made a bunch of computer parts with belts and splitters. This week, I will continue my unhealthy obsession with moving items around by making something that’s actually at least slightly practical: a balancer. Now, why would I write a whole article on designing a balancer? Well, that is because the one we will be making today is not your average balancer!
This article won’t go very deep into balancer design principles since we will be using pre-made and well-known blueprints for the most part. However, not all balancers are created equal, so you will need to know some terminology:
- Input-balanced: Draws from all inputs evenly. Especially important when merging many inputs into a few outputs.
- Output-balanced: Gives to all outputs evenly. Especially important when splitting a few inputs into many outputs.
- Throughput-limited: Has internal bottlenecks. An example of a throughput-limited system would be merging two belts into one, and then splitting it back into two. Such a system has a maximum throughput of one belt, even though two belts are available both on input and output.
- Throughput-unlimited: Opposite of throughput-limited, has no internal bottlenecks. If X belts can be going through, they will be going through.
All blueprints from this article (and a couple extras) can be found here.
The Premise
Picture the following: You’re a new player, and you’ve just heard about those things called “balancers” and how useful they are. You want to balance one belt into three. You should be using a 1-3 balancer for that, but you aren’t aware of those yet, so instead, you try to use a 4-4 balancer with only one input and three outputs hooked up. Instead of the expected 1:1:1 output ratio, you’re met with a 1:1:2 ratio and much disappointment:

With this article, I set myself the goal to make a balancer for which this sort of intuition works; In other words, no matter the input/output configuration, all outputs are always equal, and all inputs are drawn from evenly. This kind of balancer is known as a “universal balancer”, a concept first explored and named in this post by Reddit user u/tzwaan, who is one of the moderators of the Factorio subreddit.
Universal balancers can do what no balancer should be able to: no matter the configuration, they’re input-balanced, output-balanced, and throughput-unlimited at the same time! This is a set of properties previously thought to be possessed only by a 2-2 balancer, which is just a single splitter. The drawback is that they get big.
Design Principles
Let’s think about how to convert a 4-4 balancer into a 3-3 balancer. That is done by looping the extra output back into the first splitter. We will use this idea as our base principle:

We want the following behaviour: When an output starts overflowing, we want the excess items to automatically travel back into the balancer’s inputs to maintain full throughput on all outputs. How would we do that? Simple, we use priority splitters. By making their non-priority output put items onto the loop, we guarantee that the overflow, and only the overflow, go on it. We also need to merge the looping items with the inputs. For that we once again need priority splitters, but this time with input priority. We set the loop to be the non-prioritized input so that the items on the loop don’t interfere with the input in any way:

After some testing, we’ll discover a major issue. If the looping items try to enter a belt that’s already full, they just back up all the way to the split-off point and block the overflow, putting us back to square one:

To remedy this, we need to make sure every item on the loop can get to every single one of the loop’s exits. This can be done in many ways, but for our needs, we’re looking for the smallest number of splitters. It just so happens that the most splitter-economical way to do this is with another balancer. Let’s add it to the loop:

We now have a fully functional universal 4-4 balancer. However, it can be improved. Because of certain balancer mechanics, we don’t actually need four belts looping back. In general, we need three belts less than our balancer is made for. This means we can optimize our balancer by compressing the looping belts into two, and then splitting them again:
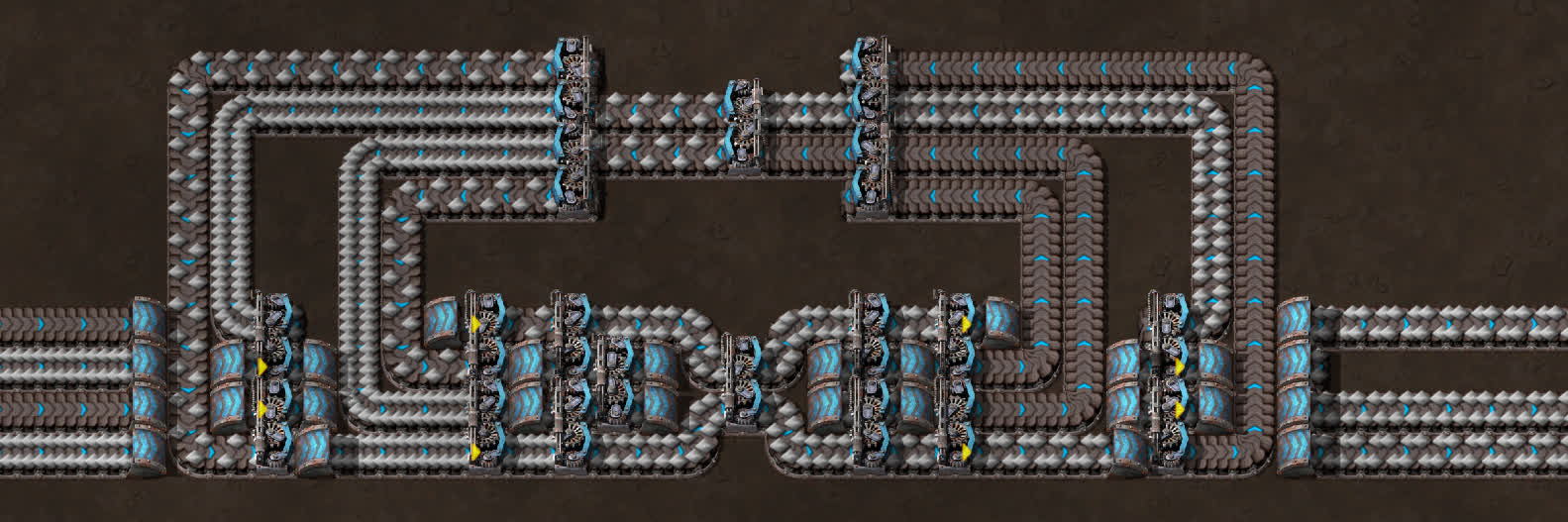
Now we can shuffle the components around until we get something small, such as this:

This balancer, while pretty long, is only six wide, which means you can fit it in a standard four belt bus, and have just enough space to tile them next to each other. It’s important to note that this is not my design (the original is by u/SirOrangeJuice), although it’s based on one of mine.
Advanced Design
Now, let’s try something bigger: a universal 8-8. We begin by doing the same steps as with our 4-4, except we use 8-8 balancers instead. This is what we get:

Unfortunately, the universal 8-8 we get this way is imperfect. Unlike the standard 4-4 balancer, the standard 8-8 balancer is throughput-limited, which makes the whole universal 8-8 balancer throughput-limited. Here is one condition which makes it bottleneck:
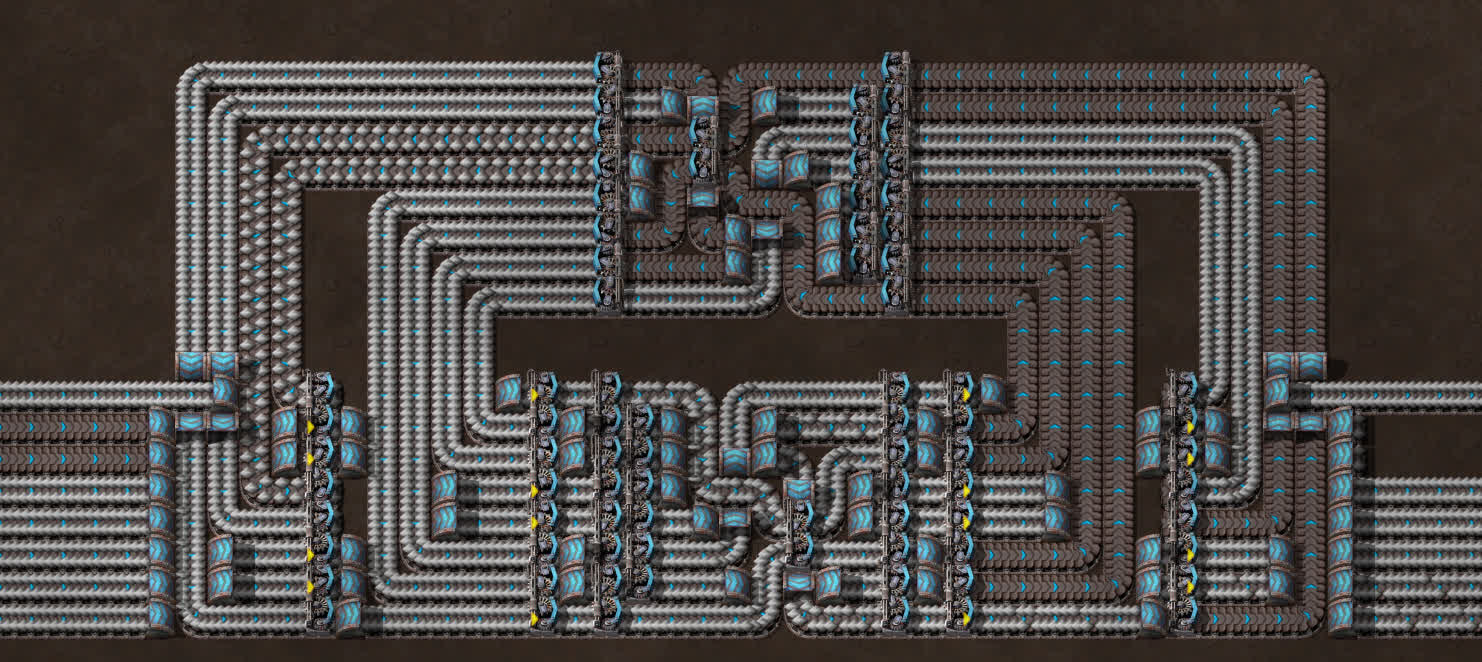
As you can see, six belts of input and output are available, but less than six are coming through. Luckily, this is easily fixed by simply replacing the core balancer with a throughput-unlimited one:

Notice how the secondary balancer can stay throughput-limited because its only job is to allow items access to all belts. Now, we could try to use our loopback compressing trick, but we’d need to compress eight belts into five, and then split back into eight. That takes way more splitters than we need if we just skip the compression and balance the eight belts directly. Since we’re using blue belts, we can employ belt weaving and squish the eight blue belts of loopback into a couple of two tile wide corridors on either side:

The whole thing is unrecognizable, but that’s because the secondary balancer is now in line with the main one, meaning we have to deal with up to twelve belts shoved into an eight tile wide space, which forces the secondary balancer to be extremely spread out. When we downgrade from blue belts to red belts, we can also ditch the belt weaving entirely, and just use a couple of blue undergrounds to get eight red belts into a space of four. This also makes it easy to downgrade to yellows, granted that we still have to use some red and blue undergrounds:
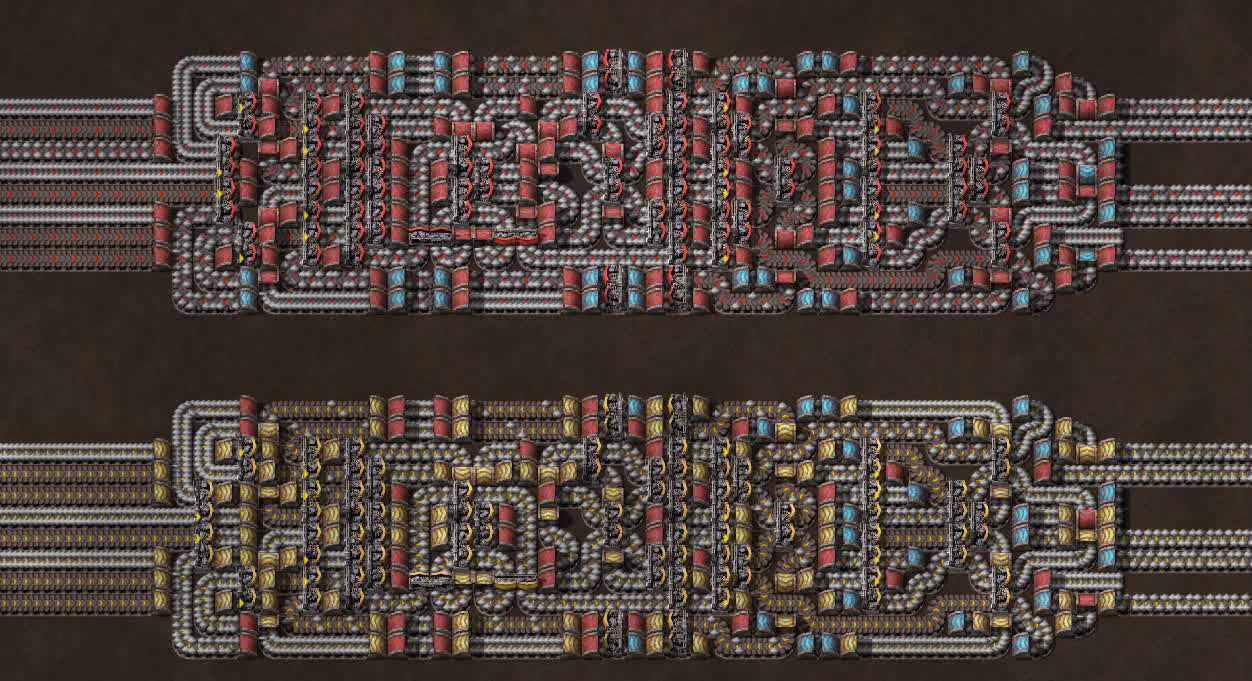
It’s definitely possible to make a yellow belt design without any blue undergrounds, but that would make the whole thing much longer. It is also possible to make both the red and yellow designs without any higher-level undergrounds at all, but that would make the whole thing 33% wider and who knows how much longer.
Final Explanations
I intentionally left some mysteries in this article, as some were too awkward to explain in the process, and some I don’t understand that well myself. This is the part where I (try to) clear them up, so fair warning that some technical stuff is coming.
- How do you know that a balancer is the most efficient way to distribute items across belts?
Let’s prove this using induction. First, imagine that we already have the most efficient possible distributor across 2N-1 belts, we’ll call it the “small distributor”. Now, let’s add a row of splitters to split each of its outputs into 2. We now have a 2N-1-2N distributor. To have the right number of inputs, let’s clone the small distributor and feed its outputs to the remaining inputs of the added row of splitters. We now have a 2N-2N distributor with the smallest possible amount of splitters. Now we just say that a 2-2 distributor is a single splitter, which is obviously the most efficient. This efficient redistributor generation algorithm is identical to the simplest possible balancer generation algorithm, and you can feel free to test that yourself.
- How do you guarantee input balancing?
For any N-N balancer, if no outputs are congested, then all of them have the same throughput regardless of inputs. Similarly, if no inputs are starved, all of them have the same throughput regardless of outputs. So long as the loopback has enough capacity to feed all the missing inputs, there will be input balancing.
- Why three fewer belts in the loopback?
To be honest, I don’t fully understand this myself. It’s an experimentally obtained result, and it has something to do with three being the smallest number that doesn’t divide 2N, which makes three open outputs the worst case the loopback has to deal with. I can’t explain why one and two don’t need full loopback throughput, though. If anyone wants to volunteer and help me out with the math here, I’d be more than grateful.
Conclusion
This has been a more or less surface-level look at the world of universal balancing. We could have taken a deeper dive, such as exploring the N-3 theorem, but I don’t think universal balancers are useful enough to warrant that. They’re really more of a fidget toy and a neat curiosity than something applicable to real problems. I can only think of two potential use cases for a universal balancer, one being loading/unloading trains with variable lengths, and the other being not wanting to scroll through blueprint books of balancers. Universal balancers (and really, all balancers) are just too big for not enough benefit, and you should be using priority-based belt compressors instead anyway. The universal 8-8 balancer is an experiment in what can be done with belts (it’s almost as if it’s a spiritual successor to the belt adder and memory) and is not intended to be used in any meaningful way. If you manage to find a niche for it, please let me know, as I am very curious myself about what this monstrosity can be useful for. You’re also welcome to try and make the presented designs smaller if you’re an absolute maniac and have way too much free time.
Contributing
As always, we’re looking for people that want to contribute to Alt-F4, be it by submitting an article or by helping with translation. If you have something interesting in mind that you want to share with the community in a polished way, this is the place to do it. If you’re not too sure about it we’ll gladly help by discussing content ideas and structure questions. If that sounds like something that’s up your alley, join the Discord to get started!