Alt-F4 n°11 - Curiosités scientifiques 30-10-2020
traduit par bev, Firerazer, relu par alarig

Sommaire
-
Un examen scientifique du monde de Factorio
pocarski - Nauvis est une naine blanche
- Quelques informations sur la mécanique orbitale de Nauvis
- Nauvis reflète au moins 88,3% de toute la lumière qui la frappe.
- Les explosions nucléaires sont extrêmement peu puissantes
- Le combustible nucléaire est trois fois plus chaud que la surface du Soleil
- Les objets ont des densités incroyablement faibles
-
Les archives de Nauvis : Techniques dépassées
stringweasel - Contribuer
Bienvenue dans la onzième édition de Alt-F4, qui vous amène des maths et de l’histoire. Donc, écoutez bien, étudiants ! Pocarski a pris sur lui-même pour aller voir si les maths du monde réel s’appliquaient bien à Nauvis. Spoiler : nope. Puis, stringweasel revient une fois de plus pour nous faire découvrir un autre aspect de l’histoire, cette fois centré sur les mécaniques oubliées, depuis longtemps obsolètes.
Un examen scientifique du monde de Factorio pocarski
La suspension de l’incrédulité est un concept bien connu, ce qui n’empêche pas certains d’entre nous de l’ignorer complètement. J’ai récemment vu un article sur Reddit sur le calcul de la densité de Nauvis, et cela m’a donné l’idée de faire une compilation juste pour le plaisir de toute la science ridicule qui se passe dans l’univers de Factorio. Après tout, cette communauté n’a toujours été qu’une bande d’intellos ayant beaucoup trop de temps libre, alors pourquoi ne pas s’adonner à un peu de nerdisme récréatif ?
Avertissement évident : cet article contient des quantités excessives de maths ; si vous avez une allergie invalidante aux maths, n’hésitez pas à le passer.
Nauvis est une naine blanche
Il s’agit d’une reprise de l’article de Reddit par u/DaveMcW que je viens de mentionner. Notez que cette théorie suppose que le cycle jour/nuit de Nauvis est en fait causé par la rotation, ce à quoi je m’opposerai plus tard.
Les grands corps célestes sont maintenus ensemble par la gravité et, pour qu’une planète ne soit pas déchirée par la force centrifuge, l’accélération gravitationnelle à l’équateur doit être supérieure à l’accélération centripète. En assumant une planète sphérique et en utilisant les équations de l’accélération centripète et de la gravité, nous pouvons montrer que :
$ \frac{GMm}{r^2} > mr\omega^2 $, où $G$ est la constante gravitationelle, $r$ et le diamètre de la planète, $M$ est la masse de la planète, $\omega$ est la vitesse angulaire de la planète, et $m$ est la masse de l’objet qui créé ces forces ;
$ \frac{GM}{r^2} > r\omega^2 \quad\Rightarrow\quad GM > r^3\omega^2 $
$ \frac{4}{3}\pi r^3 = V \quad\Rightarrow\quad r^3 = \frac{3V}{4\pi} $, où $V$ est le volume de la planète ;
$ GM > \frac{3V\omega^2}{4\pi} \quad\Rightarrow\quad G\frac{M}{V} > \frac{3\omega^2}{4\pi} $
$ \omega = \frac{2\pi}{T} \quad\Rightarrow\quad \frac{3\omega^2}{4\pi} = \frac{3\pi}{T^2};\quad \frac{M}{V} = \rho $, où $ \rho $ est la densité de la planète ;
$ \frac{G\rho}{3} > \frac{\pi}{T^2} \quad\Rightarrow\quad \rho > \frac{3\pi}{GT^2} $
Nous obtenons une expression de la densité en fonction de la période de rotation. En ajoutant les valeurs pour $ \pi $ et $G$, tout en prenant en compte la durée du cycle jour/nuit de Factorio (T = 25 000 ticks = 416.(6) secondes), on trouve :
$ \rho > 813,400 \mathrm{kg/m^3} $
La densité de Nauvis doit être supérieure à 813,400 g/cm3. À titre de comparaison, la densité de l’acier est de 8,050 g/cm3, celle du plomb est de 11,350 g/cm3, et celle de l’osmium métal, la substance la plus dense sur Terre, est de 22,570 g/cm3. 813,400 g/cm3 est un nombre si extrême que Nauvis doit être une étoile naine blanche pour être aussi dense. Pour ceux d’entre vous qui ne le savent pas, une naine blanche est ce qui reste après qu’une étoile autour de la masse du Soleil meurt et s’effondre, laissant un reste surchauffé de la taille de la Terre. Les naines blanches ont des températures de surface allant de 8 000 K à 40 000 K. En comparaison, la surface du Soleil est un peu inférieure à 6 000 K. Le sol de Nauvis doit être un isolant thermique exceptionnel !
Quelques informations sur la mécanique orbitale de Nauvis
Comme toutes les ombres sont à une longueur et une direction constantes tout au long de la journée, nous devons conclure que la position de la source de lumière dans le ciel ne change pas, ce qui signifie que Nauvis est verrouillé par effet de marée. Il s’ensuit que le cycle jour/nuit que nous observons est causé par un objet qui occulte la lumière. D’après la fréquence des nuits, cet objet est probablement en orbite autour de Nauvis, et il ne peut s’agir d’une lune, car une lune assez grande pour des nuits aussi longues capturerai Nauvis dans son orbite. La nuit doit donc être causée par un nuage de débris en orbite autour de Nauvis - ce qui explique aussi pourquoi l’ingénieur s’y est écrasé en premier lieu : le navire a heurté des roches en orbite.
Une autre explication du cycle jour/nuit, proposée par certains, est que l’étoile parente de Nauvis est une variable Céphéide, qui est un type d’étoile qui varie en taille, température et luminosité selon un schéma régulier. Personnellement, je pense que c’est impossible car la variance de luminosité est beaucoup trop élevée, surtout pour une période aussi courte.
Nauvis reflète au moins 88,3% de toute la lumière qui la frappe.
Un seul panneau solaire dans Factorio a une surface de 9 m2 et produit 60 kW pendant la journée. D’après ces chiffres, nous constatons que la surface reçoit au moins 6,(6) kW/m2 (contre 1 kW/m2 pour la Terre). Étant donné que la température ambiante de Nauvis est de 15 degrés Celsius, et qu’elle est verrouillée par effet de marée, nous pouvons utiliser une formule de température efficace légèrement modifiée :
$ T = \root{4}\of{\frac{1}{2}\frac{P(1-a)}{\sigma}} $, où $P$ est la puissance reçue par unité de surface, $T$ est la température absolue de la surface, $a$ est l’albédo (ce que nous essayons de trouver), et $\sigma$ est la constante de Stefan-Boltzmann.
$ a = 1 - \frac{2\sigma T^4}{P} $
$ T = 15\mathrm{°C} = 288,15\mathrm{K} $
$ P = 6666,(6)\mathrm{W/m^2} $
$ a = 0,8827 $
Nauvis doit avoir un albédo d’au moins 0,883 pour maintenir 15 °C. Cela signifie qu’elle reflète au moins 88,3 % de la lumière qui la frappe. Comme le rendement de nos panneaux solaires est probablement inférieur à 100%, et que Nauvis n’est probablement pas un corps noir idéal, l’albédo est probablement encore plus élevé.
À titre de comparaison, l’albédo de la Lune est de 0,14 et celui de la Terre de 0,306. Si la Lune avait un albédo de 0,883, elle serait 6,3 fois plus lumineuse. Si la Terre avait un albédo de 0,883, elle aurait une température moyenne de surface de -88,5 °C.
Les explosions nucléaires sont extrêmement peu puissantes
Il est maintenant temps de revenir de l’espace et de jeter un coup d’œil sur les choses artificielles. Un morceau d’Uranium235 de Factorio peut produire 10 piles à combustible, chacune contenant 8 GJ (ignorons le bonus du voisin). Cela signifie qu’un seul morceau d’U235 contient 80 GJ d’énergie de fission, et comme une bombe nucléaire utilise 30 morceaux d’U235, avec un taux de fission de 20 % (ce que l’on obtient avec la fission dopée; qui est nécessaire pour une si petite bombe nucléaire), elle devrait avoir un rendement explosif de 115 tonnes de TNT. Cela ne semble pas beaucoup, mais juste le graphisme d’explosion lui-même ferait 60 tuiles de diamètre. Une telle bombe nucléaire détruirait tout complètement dans un rayon de 100 tuiles, tuerait tout dans un rayon de 250 tuiles, et ferait des dégâts dans un rayon de 500 tuiles (d’après Nukemap).
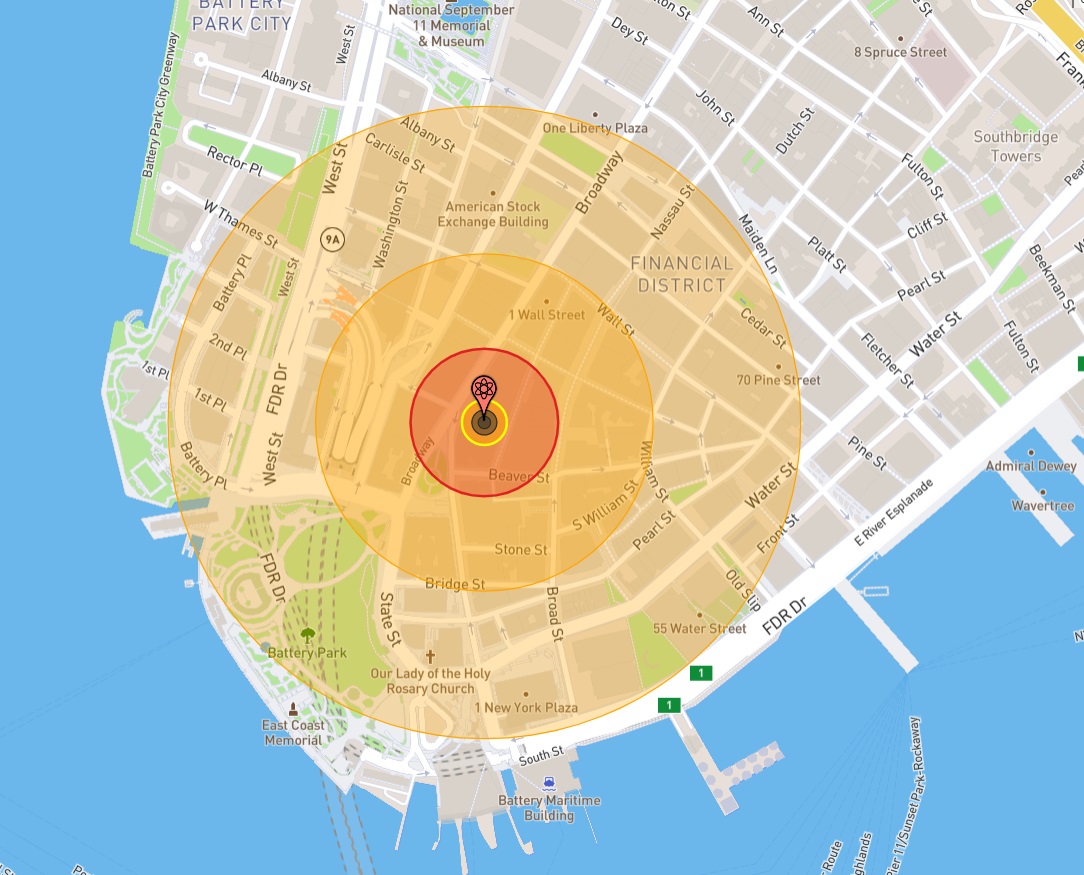
Les anneaux sur ce diagramme indiquent, du plus petit au plus grand :
- Cratère et bord du cratère (graphismes de la brûlure)
- Boule de feu (graphisme de l’explosion)
- Dommages aux structures lourdes (la zone “tout détruire complètement”)
- 100% de probabilité de brûlures au 3ème degré (la zone “tout tuer”)
- 50 % de probabilité de brûlures au premier degré (la zone “faire des dégâts”)
Pour être tout à fait honnête, si nous considérons que l’U238 contribue également à la puissance d’une pile à combustible, nous obtenons une explosion nucléaire un peu plus petite. C’est quand même dérisoire, mais un peu moins.
En parlant d’énergie nucléaire…
Le combustible nucléaire est trois fois plus chaud que la surface du Soleil
Les locomotives ont une consommation d’énergie constante de 600 kW, mais un meilleur carburant les rend plus rapides. Cela signifie qu’un carburant de meilleure qualité augmente l’efficacité du moteur.
Nous pouvons exprimer la puissance produite par l’accélération et la vitesse :
$ P = \frac{A}{t} = \frac{Fs}{t} = Fv = mav $, où $P_u$ est l’énergie utilisable, $m$ st la masse du train, $a$ est son accélération, et $v$ est sa vitesse maximale.
Si $N$ est le rendement :
$ N = \frac{P_u}{P_c} = \frac{mav}{P_c} $, où $P_c$ est l’énergie totale consommée (600 kW) ;
$ \frac{N_1}{N_0} = \frac{a_1v_1}{a_0v_0} $, où $N_0$, $a_0$, and $v_0$ sont respectivement l’efficacité, l’accélération et la vitesse maximale quand du charbon est utilisé ; $N_1$, $a_1$, and $v_1$ sont les même paramètres mais en utilisant un autre carburant.
Ainsi, le rendement du combustible divisé par le rendement du charbon est exactement égal à la nouvelle vitesse de pointe multipliée par la nouvelle accélération, ce qui signifie que le combustible nucléaire est 1,15 * 2,5 = 2,875 fois plus efficace que le charbon. Comme les locomotives peuvent fonctionner avec n’importe quel carburant, on peut supposer sans risque qu’elles utilisent un moteur thermique. Si ce moteur fonctionne aussi efficacement que possible (sur la base d’un cycle de Carnot), son rendement est de :
$ N = 1 - \frac{T_{c}}{T_{h}} $, où $T_c$ est la température absolue de la partie froide du moteur (288,15 K; la température ambiante), et $T_h$ est la température absolue de la partie chaude du moteur (chauffée par le carburant). Il est raisonnable de supposer que sur Nauvis, le charbon brûle à 165 °C (438,15 K), sur base de la température de la vapeur de la chaudière. Cela signifie que le rendement d’un train roulant au charbon est de :
$ N = 1 - \frac{288,15\mathrm{K}}{438,15\mathrm{K}} = 0,34 $
Le rendement du combustible nucléaire est 2,875 fois supérieur (voir ci-dessus), ce qui signifie qu’il est égal à 0,98. Cela signifie que :
$ 1 - \frac{288,15\mathrm{K}}{T} = 0,98 $
$ T = \frac{288,15\mathrm{K}}{1-0,98} = 18297,525\mathrm{K} = 18024,375\mathrm{°C} $
Le combustible nucléaire a donc une température de plus de 18 000 degrés Celsius. Curieusement, si la vapeur de la chaudière était seulement 3,68 degrés plus chaude, le rendement du combustible nucléaire deviendrait exactement de 1. Et s’il dépassait même un peu 168,68 °C, la physique commencerait à s’effondrer.
Mais ce n’est pas un problème si important, car tout est déjà foutu sans cela. Par exemple…
Les objets ont des densités incroyablement faibles
Cette partie est basée sur l’article Reddit de u/Maouitippitytappin sur leur voyage pour trouver les échelles dans Factorio. Pour résumer leurs propos : en connaissant la consommation d’énergie d’une fusion de base dans un four, on peut trouver la masse d’une seule plaque de fer, qui s’avère n’être que d’environ 40 grammes. De même, une plaque de cuivre pèse environ 65 grammes. (Les sources peuvent varier ; vous pourriez obtenir des résultats de recherche différents).
Sachant cela, nous pouvons calculer que les matières premières nécessaires à une seule locomotive pèsent à peine 14,6 kg. Comme la locomotive occupe un volume d’environ 24 m3 (en supposant qu’elle ait 2 m de haut d’après son aspect) elle a une densité de 0,6 kg/m3, ce qui est environ la moitié de la densité de l’air. Cela signifie que les locomotives peuvent être utilisées comme des ballons !

Peut-être Nauvis tourne-t-elle vraiment, et le fait-elle assez vite pour que la flottabilité agisse vers le bas en raison de la force centrifuge. C’est une très bonne explication du fait que vous pouvez faire tenir 240 locomotives dans un coffre de 1 m3; c’est parce qu’elles sont probablement pliables. Ce qu’elle n’explique pas, en revanche, c’est comment les trains peuvent prendre un virage dans un rayon de 12 mètres seulement tout en roulant à un peu moins de 300 km/h sans dérailler. Ils devraient connaître une accélération de près de 60 g lorsqu’ils tournent à pleine vitesse :
$ a = \frac{v^2}{r} = \frac{(82,8\mathrm{m/s})^2}{12\mathrm{m}} = 571,32\mathrm{m/s^2} = 58,26g $
Comme les rails ne sont manifestement pas inclinés, les trains doivent avoir des roues de montagnes russes, qui s’accrochent aux voies par les 3 côtés. Personnellement, j’aime beaucoup l’idée des trains de montagnes russes en ballon qui tournent à 300 km/h avec un moteur à 18 000 °C, mais peut-être que ce n’est que moi.
Les archives de Nauvis : Techniques dépassées stringweasel
Au fil des ans, Factorio a beaucoup changé. De nouveaux joueurs, de nouvelles mécaniques, de nouveaux développeurs, de nouvelles stratégies, etc. Et à mesure que les choses changent, certaines techniques de jeu sont délaissées pour faire place à des méthodes nouvelles et améliorées. Comme il y a longtemps quand Kerbals a débarqué sur Mun en utilisant seulement des ailes comme train d’atterrissage, ou quand les joueurs de Minecraft ont construit des chariots boosters pour propulser leurs wagonnets. Il existe des rituels et des techniques anciennes que nous n’utilisons plus à l’époque moderne. Je trouve toujours intéressant de regarder en arrière et de voir ce qui se faisait dans le passé, c’est donc ce que nous allons étudier ici.
Les Poteaux de la Victoire
Avant la 0.13, les déchiqueteurs avaient très peur des structures que l’on construisait. Ils n’essayaient même pas de s’étendre et de créer de nouveaux nids à proximité de tout ce qui était placé par un ingénieur sournois. Cela a conduit à l’invention d’un certain rituel par la communauté : le placement de Poteaux de la Victoire. Vous pouviez simplement placer n’importe quelle entité après avoir éliminé un nid indigène, généralement quelque chose de bon marché comme un coffre en bois ou un poteau électrique, et qui éloignait les déchiqueteurs de votre terre légitimement conquise. Il existe une superbe vidéo de NegativeRoot qui explique ce rituel. Ironiquement, après la 0.13, quand les déchiqueteurs n’ont plus eu peur de nos structures, quelques ingénieurs sans méfiance ont trouvé des nids à l’intérieur de leurs bases non défendues !

Perte de compression dans les virages
La plupart ne s’en rendent pas compte, mais le convoyeur est l’entité la plus complexe dans Factorio. Aujourd’hui, elle “fonctionne tout simplement”, mais il a fallu des années pour faire disparaître tous les bugs et les maux de tête. Des choses comme les objets qui se coincent, les bras qui ne ramassent pas le dernier objet sur le convoyeur, et les nécessaires convoyeurs souterrains qui augmentent le volume de calculs. Plus tristement célèbre, mais depuis longtemps oublié, est la perte de compression dans les virages avant la 0.12 et les techniques utilisées pour maintenir un débit de 100 %.
À l’époque, les convoyeurs perdaient de leur compression dans les virages en raison de la façon dont les collisions étaient gérées. Jadis, les objets sur les convoyeurs étaient des entités individuelles avec des boîtes de collision qui les faisaient se heurter involontairement dans les coins ; aujourd’hui, ces objets n’ont plus du tout de boîtes de collision. Même à cette époque, les joueurs voulaient bien sûr toujours construire en grand, et devaient donc contourner cette perte de compression. Pour les plus petites constructions, une compression d’environ 100 % était obtenue en remplaçant l’angle par un convoyeur de niveau supérieur ou en utilisant deux répartiteurs. Mais pour les grandes usines avec de grands bus - où les convoyeurs étaient déjà de niveau supérieur - des conceptions plus complexes étaient nécessaires. En général, ces systèmes ont été conçus par le légendaire magicien des convoyeurs MadZuri, pour être mis en œuvre dans les usines folles de ColonelWill.
De longs débats ont eu lieu sur ce que devrait être le comportement dans les virages, même après que la perte de compression ait été corrigée en 0.12. Les objets doivent-ils se déplacer à une vitesse constante, comme c’est le cas actuellement, c’est-à-dire que les objets intérieurs sortent du virage en premier ? Ou la ligne intérieure doit-elle se déplacer plus lentement afin que les lignes intérieure et extérieure restent synchronisées dans les virages ? Il s’agissait essentiellement de discuter du réalisme par opposition au jeu et, parfois par inadvertance, de la latence comparée au débit. Certains ont simplement apprécié toutes les vidéos qui ont été publiées concernant des chaînes de production réelles qui prennent des virages.
La mécanique des convoyeurs est l’un de ces domaines où, si elle n’est pas parfaite, tout le monde remarquera que quelque chose ne va pas. Mais dès qu’elle est efficace, elle passe presque inaperçue en raison de son intuitivité et de sa simplicité. En effet, une bonne mise en œuvre doit être intuitive et dissimuler l’énorme complexité qui se cache derrière avec une interface simple. Et comme vous le savez, les ingénieurs d’aujourd’hui ne font pas souvent de commentaires sur la mécanique des convoyeurs. Les convoyeurs sont faciles à utiliser et ont tout simplement du sens. Cela signifie que l’équipe de Factorio a vraiment réussi à créer l’ultime mise en œuvre des convoyeurs.
Répartiteurs à priorité manuels
Les répartiteurs ont seulement acquis la possibilité de régler une entrée/sortie prioritaire en 0.16.17 (parallèlement à l’introduction du filtrage). Avant cela, les répartiteurs à priorité devaient être construits en n’utilisant que de l’intelligence, des spaghettis et tout un tas de logique. Il en est résulté une période en 2016 où ces conceptions sont devenues un sujet brûlant dans la communauté. Des joueurs comme Steejo, raspi, canidae et Captain Konzept, pour n’en citer que quelques-uns, ont rapidement entamé des recherches et des tests approfondis pour le plus grand bien de l’usine.

La construction d’un répartiteur à priorité utilisant la logique n’a pas été facile, surtout à l’époque, mais cela n’a pas arrêté notre communauté hautement qualifiée ; elle a surmonté de nombreux obstacles avec vigueur. Par exemple, en lisant un convoyeur entièrement comprimé, elle pouvait afficher 6 ou 8 objets apparemment au hasard. Pire encore, il n’y a aucun moyen de différencier un convoyeur entièrement comprimé d’un convoyeur non comprimé. Dans les deux cas, la logique continuait à lire 8 (ou 6 !) objets sur le convoyeur. Cela a donné lieu à diverses conceptions compliquées, chacune avec ses propres trucs et astuces mis en œuvre de manière experte pour la faire fonctionner. Captain Konzept a réalisé une excellente vidéo expliquant les diverses approches des différents joueurs (et une autre vidéo comparant plus tard ces conceptions aux nouveaux répartiteurs avec les réglages de priorité intégrés).
Après un certain temps, les gens ont réalisé que dans la plupart des cas, une répartition complexe des priorités n’est pas vraiment nécessaire, et qu’un équilibre adéquat est sans doute suffisant. Cet état d’esprit a encore changé après la mise à jour des répartiteurs avec la version 0.16.17. Quoi qu’il en soit, le fait est qu’ils ont réussi à créer un répartiteur à priorité manuel ! Cependant, ce n’est pas la seule chose folle que les experts ont réussi à faire en utilisant la mécanique simple du répartiteur.
Magie noire : Filtrage mécanique par répartiteur
Comme mentionné, avant la 0.16.17 (ou 0.16.16), les répartiteurs se comportaient différemment et n’avaient pas de réglage de filtre. Cette limitation n’a cependant pas empêché la communauté de quand même abuser des répartiteurs pour filtrer les objets - cette fois sans utiliser de circuit logique ! Tout a commencé avec ce message de SPolygon disant que leur répartiteur ne se divisait pas correctement. Comme l’expliquait daniel34, le répartiteur choisissait le côté vers lequel un objet allait passer en fonction du type d’objet également, et non pas simplement en alternant entre chaque objet. Cela a piqué la curiosité du légendaire XKnight qui a immédiatement mis au point quelques prototypes qui abusent de cette mécanique. Ces conceptions semblaient frôler la magie et ont même sidéré les développeurs ! Environ un an plus tard, u/tzwaan a redécouvert le travail de XKnight, a poursuivi les recherches et l’a ensuite montré au monde de Reddit, en le baptisant filtreur d’objets de magie noire..
Il convient de rappeler que ces répartiteurs n’ont aucune capacité de filtrage intégrée. Néanmoins, les experts de la communauté pouvaient réaliser le filtrage en abusant de leur mécanique interne. À l’époque, en 2016 et 2017, la plupart des gens étaient obsédés par les répartiteurs, qu’il s’agisse du partage à priorités ou du filtrage fou de magie noire. Et au lieu de se plaindre aux développeurs d’ajouter ces mécanismes comme des fonctionnalités, ils ont travaillé ensemble pour résoudre ces problèmes communs simplement en jouant le jeu. À mon avis, c’est un témoignage de la grandeur de la communauté Factorio et du dévouement et des compétences de certains de nos joueurs.
Contribuer
Comme toujours, nous attendons vos contributions pour les Alt-F4, que cela soit par la soumission d’un article ou en aidant pour les traductions. Si vous avez quelque chose d’intéressant en tête que vous souhaitez partager avec la communauté, vous êtes donc au bon endroit. Si vous n’êtes pas sûr, nous serons heureux de vous aider en discutant structure, contenu et idées. Donc si vous voulez vous impliquer dans les Alt-F4, rejoignez-le Discord pour ne rien rater !