Alt-F4 n°23 - Spaghetti en folie 12-02-2021
traduit par Trasdegi, bev, relu par Firerazer

Après une interruption de deux semaines en raison de quelques FFF tout juste sortis de presse, nous revenons cette semaine avec deux articles sur les convoyeurs. Dans le premier, Recon419A explore un concept intéressant dans lequel les convoyeurs livrent des objets en flux tendu. Ensuite, les choses deviennent vraiment dingues lorsque Pocarski se lance dans la construction d’une machine de Turing qui n’utilise que des convoyeurs. Diplôme d’informatique recommandé !
Convoyeurs logistiques Recon419A
Dans Factorio, il y a trois méthodes principales pour déplacer des objets : les convoyeurs, les robots, et les trains. Les convoyeurs sont efficaces pour un débit moyen d’un ou deux types d’objets, les trains pour de grandes quantités d’un seul objet, et les robots pour des systèmes complexes de fabrication. Cependant, une combinaison de ces approches est parfois nécessaire, et c’est là que certaines techniques comme le convoyeur à sushi peuvent rentrer en jeu. Dans cet article, je voudrais présenter une autre approche que je nomme “convoyeurs logistiques”. Comme les convoyeurs à sushi, les convoyeurs logistiques peuvent être utilisés avec ou sans mods et ne sont pas un mod en eux-mêmes ; ils sont plutôt un moyen qui permet de contrôler où vont les objets en utilisant des convoyeurs et quelques circuits très simples. Comme le réseau logistique du jeu de base et certains mods basés sur les trains comme LTN, leur objectif est d’être un moyen de livrer des ressources de manière plus intelligente que de simplement tirer un convoyeur basique.
Description d’un convoyeur logistique
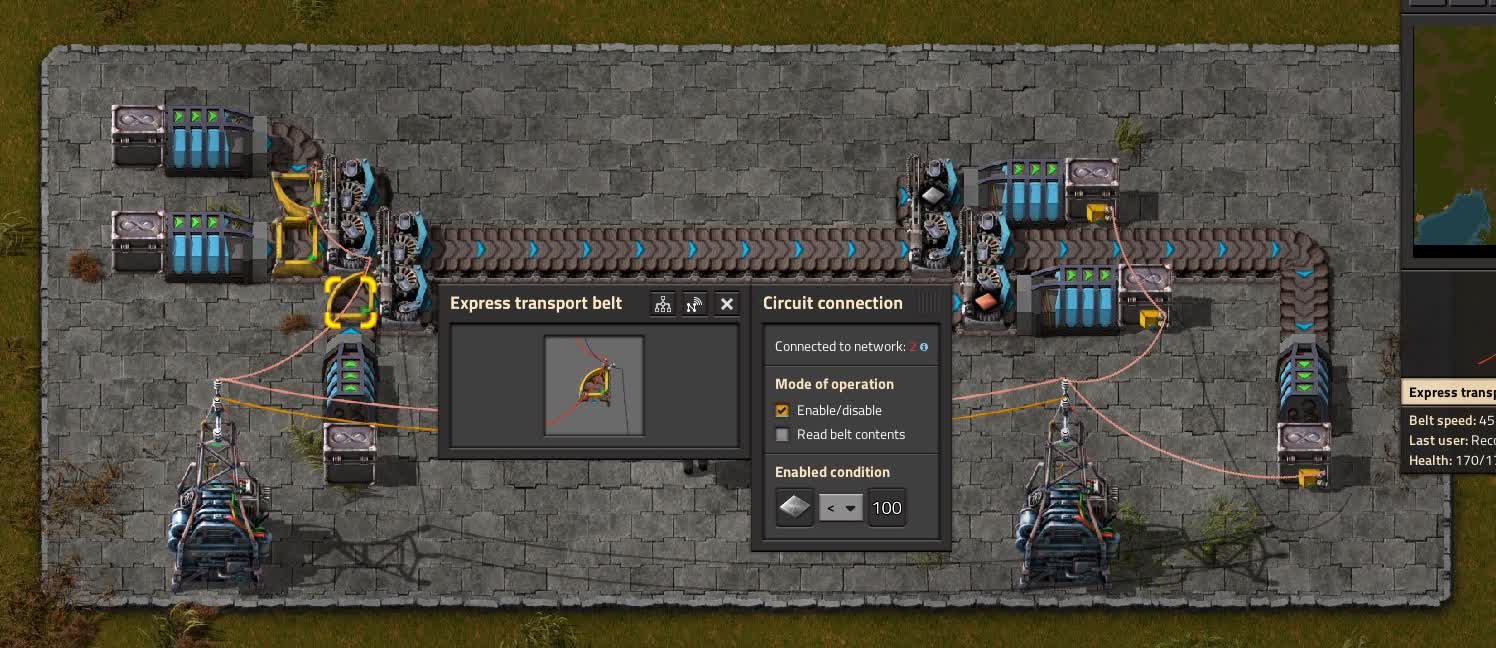
Le concept de convoyeur logistique est quelque peu compliqué, mais il est beaucoup plus simple de le comprendre en en voyant un en fonctionnement. Dans cet exemple, remarquez que plusieurs objets différents sont envoyés par le même convoyeur, chacun étant chargé sur le convoyeur uniquement quand il est demandé. S’il n’y a besoin que de fer et de cuivre, l’acier ne sera pas envoyé ; de même, si rien n’est nécessaire, le convoyeur restera vide.
Vous pouvez voir dans cet exemple que la condition logique est réglée pour envoyer des matériaux quand la destination en a moins de 100. En pratique, la longueur du convoyeur affectera la quantité de matériaux envoyée ; si le convoyeur est long, quand 100 objets seront arrivés, il en restera des centaines en chemin. Il y a une limite théorique de longueur imposée par la capacité du coffre qui reçoit les objets, mais en pratique, elle ne sera jamais atteinte si des coffres en acier sont utilisés ; et vous utiliserez de toute façon des trains pour les très longues distances. Si vous voulez bidouiller avec ce concept de convoyeur logistique, la chaîne de partage du plan est disponible ici, veuillez cependant noter que ce plan utilise les chargeurs du mod Loader Redux.
Applications des convoyeurs logistiques
Les convoyeurs logistiques sont utiles lorsque des grandes quantités d’un objet sont nécessaire au même moment, mais très peu souvent. Quiconque ayant déjà automatisé la production de convoyeurs avec des robots connaît bien le problème du “nuage de chargement” survenant quand votre réseau logistique demande pas moins de 10 000 engrenages et 15 000 circuits électroniques. De même, si vous demandez, par exemple, les matériaux pour fabriquer un réacteur nucléaire ou un silo à fusée, les robots auront tendance à s’amasser autour d’une machine d’assemblage dans une zone qui n’a jamais été conçue pour cette quantité de robots. Quand vous avez besoin de grandes quantités d’un objet, il est beaucoup plus simple de l’acheminer par convoyeur : envoyer 10 000 engrenages prend moins de quatre minutes et a un impact négligeable sur les performances ; avec des robots, cela prendrait 2500 voyages et va probablement faire décoller autant de robots, submergeant la capacité de rechargement qui n’a peut-être jamais été conçue pour cela, et prenant une éternité à retourner à l’équilibre. Avoir un convoyeur dédié à chaque objet a, cependant, ses propres inconvénients ; souvent, les convoyeurs seront inutilisés et ne feront rien d’autre que prendre de la place dans votre usine, place qui peut dès le début n’être même pas suffisante pour construire un bus à 8 pistes. Pour alimenter des constructions comme un magasin, envoyer une grande cargaison d’engrenages mélangée à une grande cargaison de circuits électroniques avec un convoyeur logistique est trivial ; quand les composants sont déjà livrés sur place, utiliser des robots en interne cause beaucoup moins de pression sur le réseau logistique.
Limitation : destinations multiples
Le problème consistant à envoyer un objet vers plusieurs destinations est loin d’être trivial, et je n’ai pas personnellement réussi à le résoudre. Comme les répartiteurs à filtre extraient l’intégralité d’un objet, laisser cet objet traverser ce répartiteur uniquement à certains moments nécessite des arrangements complexes de répartiteurs et plusieurs conditions logiques provenant de différentes destinations. J’ai passé beaucoup de temps à réfléchir à ce problème, et bien que j’aie réalisé plusieurs prototypes, la plupart ont tendance à souffrir de problèmes comme des embouteillages ou le fait d’envoyer trop d’objets à une des destinations, pouvant causer un débordement si laissé sans surveillance. Cependant, la communauté Factorio étant ce qu’elle est, je ne serais pas surpris que ces problèmes soient résolus en une ou deux semaines, et ceci de plusieurs façons différentes ; peut-être pourra-t-on même vous lire présenter votre solution dans un prochain Alt-F4. Mais pour le moment, je laisse cela comme un défi pour la communauté. Pensez à me présenter vos idées !
Une remarque sur les convoyeurs à sushi
Ceux qui jouent depuis un moment auront peut-être déjà rencontré un concept similaire : les convoyeurs à sushi. Comme les convoyeurs logistiques, ceux-ci placent plus de deux ressources sur un convoyeur, mais ce sont la plupart du temps des boucles destinées à faire des fabrications complexes. Une condition logique à l’entrée ou tout autour du convoyeur aide à contrôler la quantité de chaque ressource présente, conduisant même à des exemples complexes comme le “bloodbus” - un système circulatoire pour votre usine. Même si le concept de base est similaire, les convoyeurs logistiques ont quelques différences importantes, et la principale est leur fonction : alors que les convoyeurs à sushi entourent et livrent à plusieurs machines sans ordre particulier, les convoyeurs logistiques vont vers un endroit pour y livrer des ressources depuis un autre. En fait, un convoyeur logistique peut être utilisé pour approvisionner un convoyeur à sushi à la place d’un bus ordinaire - quand des ressources sont nécessaires, elles peuvent être envoyées, avec un contrôle de flux précautionneusement limité qui empêche tout débordement de la boucle. D’autres concepts comme les convoyeurs cadencés ou la limitation des bras robotisés peuvent être utilisés ici, et même combinés avec les convoyeurs logistiques pour créer des merveilles d’ingénierie. Dans ma conception, les convoyeurs logistiques sont un élément comme un autre de la boîte à outils du joueur.
L’informatique par convoyeurs, Première partie : Des maths pas si rapides pocarski
Avec Factorio, nous pouvons utiliser le réseau logique pour construire des systèmes informatiques, en commençant par une simple logique booléenne, jusqu’à un ordinateur pleinement fonctionnel, et ensuite, quelqu’un d’assez fou pourrait même y faire tourner DOOM dessus. Ce qui est moins évident, cependant, c’est le fait que le réseau logique n’est pas le seul système complet au sens de Turing (jetez un œil à cette page pour en savoir plus) dans le jeu. En effet, vous pouvez construire un ordinateur à partir de quelque chose de très basique, quelque chose que vous obtenez presque dès que vous commencez une nouvelle partie : les convoyeurs.
Dans ce feuilleton en deux parties, je vais parcourir le processus de conception de deux systèmes utilisés dans des ordinateurs réels, avec seulement des convoyeurs et des répartiteurs. J’utiliserai des chargeurs et des coffres infinis, mais à tout moment, il y a exactement autant d’objets qui entrent que d’objets qui sortent, donc tous les convoyeurs peuvent aussi être connectés en boucle grâce à des tampons. J’ai choisi cependant de ne pas le faire par souci de place et pour éviter les spaghetti. Je dois rendre hommage à letao12 qui a réalisé une série de vidéos consacrées à la création d’un processeur exclusivement à base de convoyeurs, ce qui m’a incité à revenir sur son idée avec ma propre vision des choses.
Pour qu’un système soit complet au sens de Turing, il doit être possible de créer ce qu’on appelle des portes logiques. Les portes logiques sont des éléments simples qui effectuent les opérations de base de l’algèbre booléenne en fournissant un résultat basé uniquement sur les données en entrée au même moment. Il n’y a que 2 nombres en algèbre booléenne : 1 et 0. En électronique, ils correspondent à la tension haute et à la tension basse mais, dans notre cas, nous dirons que le convoyeur avec des objets équivaut à un 1, et le convoyeur vide à un 0. Il y a 3 portes logiques de base :
- Porte OU - donne 1 si au moins une entrée est à 1
- Porte ET - donne 1 si toutes les entrées sont à 1
- Porte NON - donne 1 seulement si l’entrée est à 0
Le tableau de vérité ci-dessous présente leurs résultats respectifs en fonction des différentes entrées possibles.
| A | B | NON A | A OU B | A ET B |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 |
On sait qu’en enchaînant ces portes logiques de manière particulière (et parfois en rebouclant certains fils), il est possible de construire une machine de Turing. Les trois types de portes de base peuvent être créés entièrement à partir de convoyeurs et de répartiteurs. Voici un lien vers un livre de plans avec tout ce qui est mentionné dans cet article, pour ceux qui voudraient expérimenter cela eux-mêmes. Je désignerai les différents objets par “type d’objet 1/2/3/…”, pour des raisons de commodité et de généralité, et par facilité les entrées et sorties prioritaires/non prioritaires par “primaires/secondaires”. J’utiliserai également des couleurs différentes dans les images, pour différencier les types d’objets.
Les portes de base
Les portes ET et OU sont aussi simples qu’un unique répartiteur avec un réglage de priorité :
La porte NON est un peu plus difficile à réaliser, mais elle peut être obtenue en utilisant plus d’un type d’objet ainsi qu’un filtrage et une priorisation intelligents :
Quand l’entrée A est à 0, le premier répartiteur ne reçoit qu’une seule entrée, et donc l’objet de type 2 va vers la sortie primaire, ce qui signifie que seule la sortie NON A est à 1. Quand l’entrée A est activée, le premier répartiteur reçoit maintenant 2 entrées ; l’objet de type 1 va vers l’entrée primaire, donc il est envoyé vers la sortie primaire, remplaçant l’objet de type 2 qui sort maintenant par la sortie secondaire. La sortie secondaire est en fait une copie de A, mais avec un type d’objet différent.
La sortie primaire du premier répartiteur est toujours 1 mais change de type d’objet en fonction de l’entrée. En utilisant un filtre, nous pouvons diviser ce signal de type d’objet variable en deux fils : l’un sera juste le signal A passant directement avec le même type d’objet que l’entrée originale (type 1) l’autre sera NON A, avec le type d’objet 2.
Ce second circuit est particulièrement utile car il combine une porte NON, un duplicateur de signaux et un échangeur d’objets. Nous avons besoin de duplicateurs de signaux car la séparation d’un convoyeur par un répartiteur supprime la saturation du flux d’objets, ce qui entraîne une interaction incorrecte avec les autres répartiteurs en générant des signaux ni à 0 ni à 1. Nous avons également besoin d’échangeurs d’objets, car il y a souvent une discordance entre le type de sortie d’un circuit et le type d’entrée d’un autre.
Le demi-additionneur
Maintenant que nous avons nos 3 composantes de base, construisons un demi-additionneur. Pourquoi avons-nous besoin d’un demi-additionneur ? Eh bien, comme son nom l’indique, un demi-additionneur est la moitié d’un additionneur complet, qui est un circuit capable d’additionner des nombres binaires. Cela nous permettra de faire des additions, et les utilisations créatives de l’addition nous aideront à mettre en œuvre littéralement toutes les autres opérations mathématiques imaginables.
Un demi-additionneur est un circuit qui additionne deux nombres binaires d’un seul chiffre. Cela peut sembler une tâche ardue, mais en réalité, c’est très simple. Les entrées A et B sont toutes deux des nombres binaires à un chiffre, ce qui signifie que la sortie maximale possible est 2 (1+1), ce qui, malheureusement, ne peut pas entrer dans une sortie à un seul chiffre. Nous utiliserons donc plutôt un nombre binaire à deux chiffres dont le premier chiffre a une valeur de 2 (21) et le second une valeur de 1 (20). En tenant compte de cela, voici la table de vérité du demi additionneur :
| A | B | 1er chiffre de A + B | 2ème chiffre de A + B |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
On peut voir que le premier chiffre est simplement donné par A ET B. Cependant, pour le deuxième chiffre, nous avons besoin de quelque chose appelé Porte XOR (XOR signifie “OU exclusif”). Une porte XOR produit un 1 si exactement une seule entrée est à 1, ce qui est précisément ce dont nous avons besoin pour le deuxième chiffre.
La logique d’une porte XOR est “A ou B, mais pas les deux”, et donc une porte XOR est simplement (A OU B) ET NON (A ET B). Voici comment faire tout cela avec les portes de base dont nous avons parlé plus haut :
Notez que nous obtenons également la sortie de la porte ET gratuitement grâce au circuit combiné Duplicateur-NON, ce qui nous donne un demi-additionneur complet. Il se trouve que nous pouvons combiner le premier échangeur d’objets avec la deuxième porte ET, ce qui nous permet de nous débarrasser d’un répartiteur :
Le produit final
Maintenant, pour convertir notre demi-additionneur en un additionneur complet, nous devons en connecter deux en séquence (d’où le nom “demi-additionneur”) :
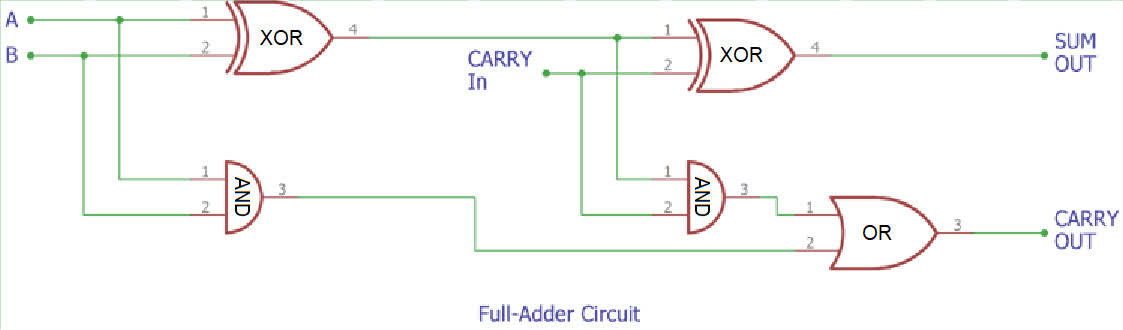
Comme vous pouvez le voir, un additionneur complet n’est que deux demi-additionneurs enchaînés d’une manière particulière. Maintenant, on pourrait simplement copier et coller le circuit, mais grâce aux propriétés des convoyeurs, il existe une méthode bien meilleure et plus compacte. Les 2 lignes d’un convoyeur sont traitées par les répartiteurs indépendamment l’une de l’autre, ce qui signifie qu’au lieu d’enchaîner deux demi-additionneurs, on peut faire passer le tout deux fois par un seul et même demi-additionneur. C’est normalement impossible avec les circuits logiques traditionnels, mais dans ce nouveau monde courageux des ordinateurs en Factorio, tout est possible. Voici comment :
Ici, le premier demi-additionneur utilise le côté droit du convoyeur, et le second demi-additionneur utilise le côté gauche du convoyeur. Tout d’abord, les entrées passent par le premier demi-additionneur comme d’habitude, sur le côté droit du convoyeur. Ensuite, la sortie XOR du demi-additionneur est ramenée jusqu’au début et est maintenant envoyée sur le côté gauche du convoyeur. Elle passe à nouveau par les mêmes mécanismes, mais comme elle est du côté gauche, elle n’interagit pas du tout avec le côté droit. Le deuxième demi-additionneur a toujours une entrée libre, et nous pouvons donc y connecter un troisième convoyeur en entrée, cette fois-ci sur le côté gauche, pour permettre la prise en compte d’un bit issu d’un calcul précédent. Les sorties ET des deux demi-additionneurs sont chargées latéralement sur un convoyeur, créant automatiquement un OU. Des retards internes peuvent entraîner une sortie simultanée des deux demi-additionneurs, ce qui fait que le système tente de transférer un convoyeur complet sur une moitié de convoyeur. C’est pourquoi nous avons également besoin d’un répartiteur de protection contre les débordements afin que le bit de sortie ne fasse pas marche arrière et ne vienne pas perturber l’ensemble du circuit. Après un réaménagement des composants, nous obtenons ceci :
C’est exactement le même circuit que dans l’image précédente, et je laisse au lecteur le soin de le vérifier. La seule chose qu’il reste à faire est d’empiler un tas de ces circuits et de leur fournir des nombres. Voici donc un additionneur à convoyeurs qui calcule 01001101 (77) + 10001011 (139) = 011011000 (216) :
Faire des additions, c’est cool comme idée, mais ce n’est rien sans une sorte de mémoire, et c’est exactement ce que nous allons explorer dans le prochain numéro. Restez à l’écoute !
Contribuer
Comme toujours, nous attendons vos contributions pour les Alt-F4, que cela soit par la soumission d’un article ou en aidant pour les traductions. Si vous avez quelque chose d’intéressant en tête que vous souhaitez partager avec la communauté, vous êtes au bon endroit. Si vous n’êtes pas sûr, nous serons heureux de vous aider en discutant structure, contenu et idées. Donc si vous voulez vous impliquer dans les Alt-F4, rejoignez-le Discord pour ne rien rater !