Alt-F4 #23 - Esteiravanza 12-02-2021
traduzido por FeLLPS

Depois de um hiato de duas semanas devido a alguns lançamentos quentes da FFF, estamos de volta esta semana com dois artigos sobre esteiras. No primeiro, o Recon419A explora um conceito interessante que faz com que os esteiras entreguem itens just-in-time. Então, as coisas ficam verdadeiramente nerds quando Pocarski dá um mergulho profundo na construção de uma máquina de turing usando apenas esteiras. É Recomendado um diploma em Ciências da Computação!
Esteiras Logísticas Recon419A
O Factorio tem três métodos principais de movimentação de itens: esteiras, robôs e trens. As esteiras são boas para o processamento de um ou dois itens, trens para grandes quantidades de um único item e robôs para tarefas complicadas de fabricação. Às vezes, no entanto, você precisa de uma combinação dessas abordagens, que é onde técnicas como esteiras sushi podem entrar em ação. Neste artigo, quero falar sobre outra abordagem que chamo de “esteiras logísticas”. Como as esteiras sushi, as esteiras de logística podem ser usadas com ou sem mods e não são um mod em si; em vez disso, elas são uma maneira de controlar quais recursos vão para onde usando esteiras e circuitos muito simples. Como a rede de logística padrão e certos mods baseados em trens como o LTN, elas visam ser uma forma mais inteligente de fornecer recursos do que simplesmente operar esteiras básicas.
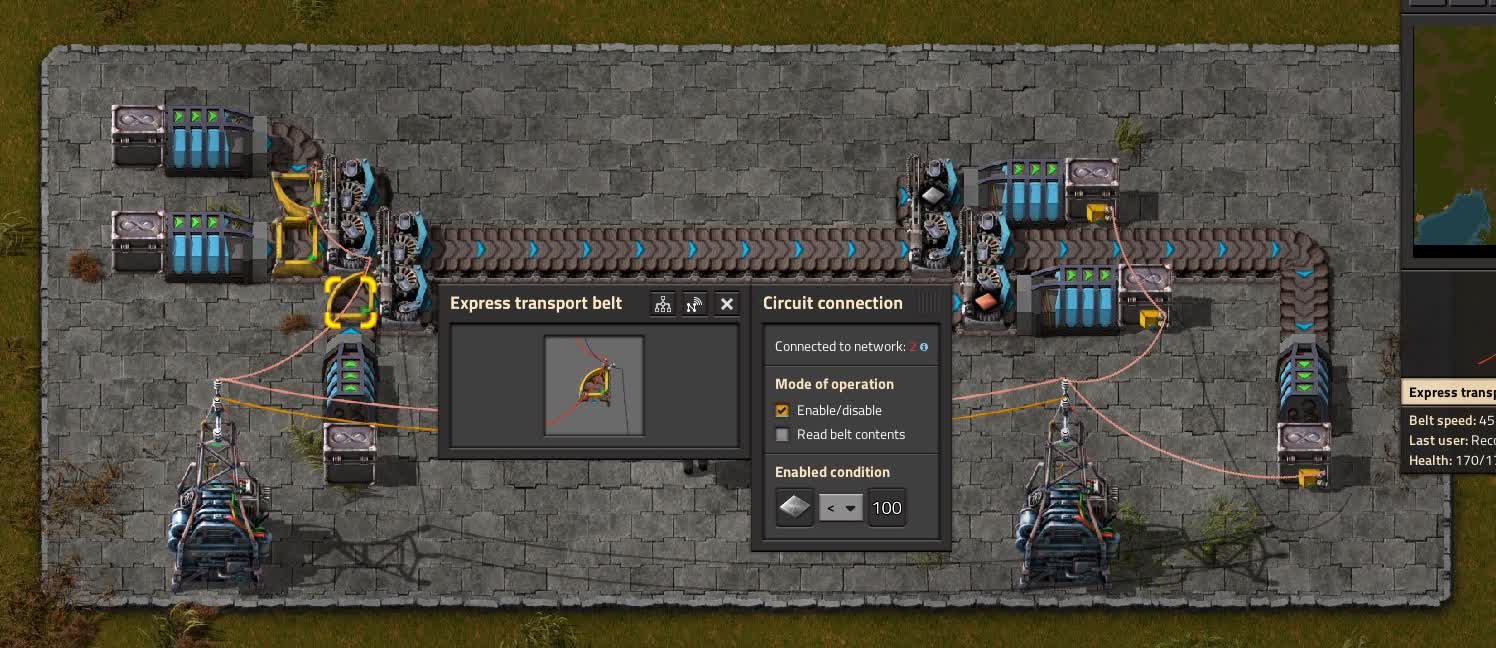
Descrição de uma esteira logística
Esteiras logísticas são um conceito um tanto complicado, mas é muito mais simples de entender quando você as vê em ação. Neste exemplo, preste atenção em como vários itens são enviados ao longo da mesma esteira, cada um sendo carregado na esteira apenas quando solicitado. Se tudo o que for necessário for ferro e cobre, nenhum aço será enviado; da mesma forma, se nada for necessário, a correia permanecerá vazia.
Você pode ver no exemplo que a condição do circuito está configurada para enviar materiais quando o destino tiver menos de cem unidades. Na realidade, o comprimento da correia afetará a quantidade de materiais enviados; se a esteira for longa, cem serão protegidos com centenas ainda na esteira. Há um limite teórico para o comprimento da esteira sem transbordar o baú do receptor, mas na prática, você não vai atingi-lo se estiver usando baús de aço; em distâncias muito longas, você usará trens de qualquer maneira. Se você tem interesse em usar esta configuração de esteira logística, a sequência de diagrama está disponível aqui, embora deve-se observar que o diagrama utiliza carregadores do mod Loader Redux.
Casos de uso para Esteiras Logísticas
As esteiras logísticas são úteis quando você precisa de muitos itens de uma só vez e depois nenhum por muito tempo. Qualquer pessoa que já tenha automatizado esteiras com robôs estará familiarizada com o fenômeno conhecido como “nuvem de recarga”, que surge quando sua rede de logística pede nada menos que dez mil engrenagens e mil e quinhentos circuitos eletrônicos. Da mesma forma, quando você pede algo como os materiais para fazer um reator nuclear ou um silo de foguete, os robôs tendem a se aglomerar em torno de um montador em uma área que nunca foi projetada para aquele grau de rendimento. Quando você precisa de muito de um item é muito mais fácil pega-lo da esteira: o envio de dez mil engrenagens leva menos de quatro minutos e quase não danifica seu UPS; com robôs, seriam necessárias 2.500 viagens separadas e provavelmente muitos robôs iriam para o ar, sobrecarregando a capacidade de recarga que talvez nunca tivesse sido projetada para isso e demorando uma eternidade para retornar ao equilíbrio. Usar esteiras dedicadas para cada item, entretanto, cria seu próprio conjunto de problemas; frequentemente, as esteiras ficarão ociosas e ocupando espaço dentro de sua fábrica e pode ser de você nem mesmo ter espaço para operar um barramento de oito esteiras. Para algo como o seu shopping de esteiras, enviar uma grande carga de engrenagens misturadas com uma grande carga de circuitos eletrônicos é trivial para uma esteira logística; uma vez que elas chegam naquele local, usar robôs internamente demanda muito menos da sua rede de logística.
Limitação: Vários Destinos
O problema de enviar um item para vários destinos não é trivial e é algo que pessoalmente não fui capaz de resolver. Como os divisores de filtro retiram todos de um item, enviar esse item além de um divisor de filtro apenas algumas vezes requer arranjos de divisores complicados e várias condições de circuito originadas de destinos diferentes. Pensei muito no problema e, embora tenha criado vários protótipos, eles costumam ser propensos a comportamentos como bloqueio ou envio de muitos itens para o destino errado, potencialmente causando um estouro se deixado sem vigilância. Com a comunidade Factorio sendo o que é, eu não ficaria surpreso se isso fosse resolvido em uma ou duas semanas e de várias maneiras diferentes; talvez até mesmo ouçamos sobre sua solução em um futuro Alt-F4. Por enquanto, porém, deixo isso como um desafio para a comunidade. Não se esqueça de me dizer o que você propor!
Uma nota sobre as Esteiras Sushi
Os jogadores que já estão no jogo há algum tempo podem já ter encontrado um conceito semelhante: esteiras sushi. Como as esteiras logísticas, as esteiras sushi colocam mais de dois recursos em uma esteira, mas geralmente o fazem como um loop projetado para criações complicadas. Uma condição de circuito na entrada ou ao redor de todo o loop ajuda a controlar a quantidade de cada recurso presente, mesmo levando a exemplos complicados como o “bloodbus” - um sistema circulatório para sua fábrica. Embora o conceito de esteira logística seja semelhante ele tem algumas diferenças importantes e a principal está relacionada à sua função: enquanto as esteiras sushi vão ao redor e tendem a atender a vários montadores em nenhuma ordem específica, as esteiras logísticas vão para e tendem a direcionar recursos de um local para outro. Na verdade, uma esteira logística pode ser usada para alimentar uma esteira sushi no lugar de um barramento comum - quando os recursos são necessários, eles podem ser enviados, com controle de taxa cuidadosamente limitados, evitando superpopulação no loop de esteira. Outros conceitos como esteiras com clock ou limitador de inserção podem ser aplicados aqui e podem até mesmo ser combinados com esteiras logísticas para alcançar feitos monumentais de engenharia. Na minha opinião, as próprias esteiras logísticas são apenas uma parte do kit de ferramentas do jogador.
Computação somente de esteiras, Parte 1: Matemática não tão rápida pocarski
Em Factorio, podemos usar a rede de circuitos para construir sistemas, começando com alguma lógica booleana simples, até um computador totalmente funcional e então alguém maluco pode até rodar DOOM nele. O que é menos óbvio, entretanto, é o fato de que a rede de circuitos não é o único sistema Turing completo (dê uma olhada na página vinculada se você não estiver familiarizado) no jogo. Na verdade você pode construir um computador a partir de algo muito básico, algo que você obtém assim que começa um novo jogo: esteiras.
Nesta série de duas partes, estarei percorrendo o processo de projeto de dois sistemas usados em computadores da vida real com nada além de esteiras e divisores. Eu estarei usando carregadores e baús infinitos, entretanto, em todos os momentos existem exatamente o mesmo número de itens entrando quanto número itens saindo, então todas as esteiras também podem fazer loop por um buffer. Eu escolhi não fazer isso por uma questão de compactação e evitando espaguete. Tenho que dar crédito a letao12 que fez uma série de vídeos sobre a criação de uma CPU apenas de esteiras, que foi o que me inspirou a voltar para sua ideia com minha própria opinião sobre isso.
Para que qualquer sistema seja Turing completo é necessário ser possível criar algo conhecido como portas lógicas. As portas lógicas são elementos simples que realizam operações básicas de álgebra booleana, fornecendo uma saída baseada apenas nas entradas atuais. Existem apenas 2 números na álgebra booleana: 1 e 0. Na eletrônica, eles correspondem a alta e baixa tensão, mas, em nosso caso, diremos que uma esteira com itens é 1 e uma correia vazia é 0. Existem 3 portas lógicas básicas:
- Porta OU – A saída será 1 se pelo menos uma entrada é 1
- Porta E – A saída será 1 se todas as entradas são 1
- Porta Não – A saída será 1 somente se a entrada é 0
A tabela verdade abaixo mostra suas respectivas saídas com base na gama de entradas possíveis.
| A | B | NÃO A | A OU B | A E B |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 |
É um fato conhecido que encadeando essas portas lógicas de maneiras específicas (e às vezes fazendo um loop em alguns fios), é possível construir uma máquina de Turing. Todos os três tipos básicos de portão podem ser criados inteiramente com esteiras e divisores. Aqui está um link para um livro de diagramas com tudo deste artigo, para quem quiser experimentar os próprios circuitos. Vou me referir a diferentes itens como “tipo de item 1/2/3/…”, por conveniência e generalidade, e entradas e saídas prioritárias/não-prioritárias como “primária/secundária”, também por conveniência. Também estarei usando cores diferentes nas imagens, para diferenciar os tipos de itens.
As portas básicas
As portas E e OU são tão simples quanto um único divisor com uma prioridade definida:
A porta NÃO é um pouco mais complicada de se fazer, mas pode ser feita usando mais de um tipo de item e alguma filtragem inteligente e priorização:
Embora a entrada A seja 0, o primeiro divisor está recebendo apenas uma entrada e, portanto, o tipo de item 2 vai para a saída primária, o que significa que apenas a saída NÃO A é 1. Quando a entrada A está ligada, o primeiro divisor está agora obtendo 2 entradas; O tipo de item 1 vai para a entrada primária, portanto, é colocado na saída primária, substituindo o tipo de item 2, que agora está saindo da saída secundária. A saída secundária é efetivamente uma cópia de A, mas com um tipo de item diferente.
A saída primária do primeiro divisor é sempre 1, mas muda o tipo de item dependendo da entrada. Usando um divisor de filtro, podemos dividir este sinal de tipo de item variável em 2 fios: um será apenas o sinal A vindo direto com o mesmo tipo de item que a entrada original, tipo 1, o outro será NÃO A, com item tipo 2.
Este segundo circuito é excepcionalmente útil porque combina uma porta NÃO, um duplicador de sinal e um trocador de item. Precisamos de duplicadores de sinal porque ramificar o sinal com uma esteira e um divisor torna o fluxo de itens insaturado, o que faz com que ele interaja com outros divisores incorretamente, pois não é 0 e nem 1. Também precisamos de trocadores de item, pois muitas vezes há uma incompatibilidade entre o tipo de saída de um circuito e o tipo de entrada de outro.
O meio-somador
Agora que temos nossos 3 componentes básicos, vamos construir um meio-somador. Por que precisaríamos de um meio-somador? Bem, como o nome sugere, um meio-somador é a metade de um somador completo, que é um circuito com a capacidade de somar números binários. Isso nos permitirá fazer adição e os usos criativos da adição nos permitem implementar literalmente todas as outras operações matemáticas imagináveis.
Um meio-somador é um circuito que soma dois números binários de um dígito. Isso pode parecer uma tarefa difícil, mas na realidade, é muito simples. Ambas as entradas A e B são números binários de um dígito, o que significa que a saída máxima possível é 2 (1 + 1), que, infelizmente, não caberá em uma saída de um dígito. Em vez disso, usaremos um número binário de dois dígitos, onde o primeiro dígito tem um valor de casa de 2 (2 1) e o segundo um valor de casa de 1 (20) Levando isso em consideração, aqui está a tabela de verdade do meio-somador:
| A | B | Primeiro digito de A + B | Segundo digito de A + B |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Podemos ver que o primeiro dígito é simplesmente A E B. No entanto, para o segundo dígito, precisamos de algo chamado de porta XOR (XOR significa “OU exclusivo”). Uma porta XOR gera 1 se exatamente uma entrada for 1, que é exatamente o que precisamos para o segundo dígito.
A lógica de uma porta XOR é “A ou B, mas não ambos” e, portanto, uma porta XOR é apenas (A OU B) E NÃO (A E B). Aqui está como fazer isso com as portas básicas discutidas anteriormente:
Observe que também obtemos a saída da porta E de graça graças ao circuito combinado duplicador-NÃO, o que nos dá um meio-somador completo. Acontece que podemos combinar o primeiro trocador de item com a segunda porta E, o que nos permite eliminar um divisor:
O produto final
Agora, para converter nosso meio-somador em um somador-completo, precisamos conectar 2 deles em sequência (daí o nome “meio-somador”):
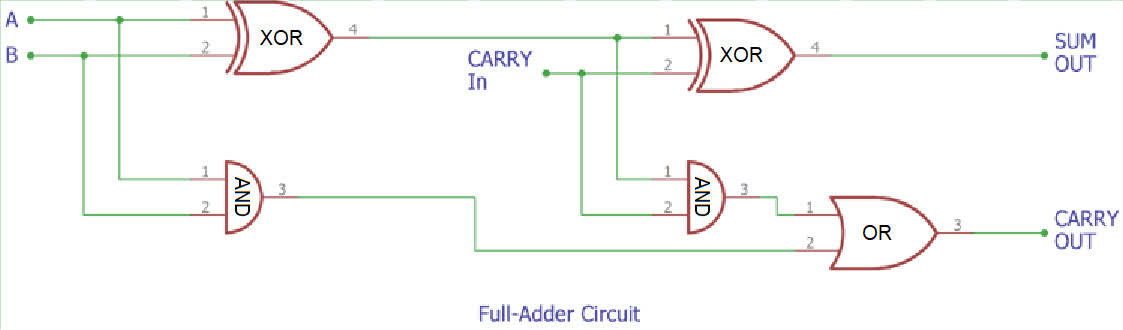
Como você pode ver, um somador-completo é apenas 2 meio-somadores encadeados de uma maneira específica. Agora, poderíamos apenas copiar e colar o circuito, mas graças às propriedades das esteiras, existe uma maneira muito melhor e menor. As 2 vias de uma esteira são processadas por divisores independentemente uma da outra, o que significa que, em vez de encadear dois meio-somadores, podemos executar tudo por meio de um único meio-somador duas vezes. Isso geralmente é impossível com circuitos lógicos tradicionais, mas neste admirável mundo novo dos computadores de Factorio, vale tudo. Aqui está como:
Aqui, o primeiro meio-somador usa a via do lado direito da esteira e o segundo meio-somador usa a via do lado esquerdo da esteira. Primeiro, as entradas passam pelo primeiro meio-somador normalmente na via do lado direito da esteira. Em seguida, a saída XOR do meio-somador é retornada totalmente e agora é colocada na via do lado esquerdo da esteria. Ele passa pelos mesmos mecanismos novamente, mas como está na via do lado esquerdo, não interage de forma alguma com a via do lado direito. O segundo meio-somador ainda tem uma entrada livre, portanto, temos que conectar uma terceira esteira de entrada, desta vez na via do lado esquerdo para agir como o bit carry in. As saídas E de ambos os meio-somadores são carregadas lateralmente em uma esteira, criando automaticamente um OU. Atrasos internos podem fazer com que os carregamentos de ambos os meio-somadores saiam ao mesmo tempo, fazendo com que eles tentem descarregar uma esteira completa na metade de uma correia. Portanto, também precisamos de um divisor de proteção contra estouro para que o carry não volte e interrompa todo o circuito. Depois de alguns rearranjos dos componentes, obtemos o seguinte:
Este é exatamente o mesmo circuito da imagem anterior, e deixo como um exercício para o leitor verificar isso. A única coisa que resta a fazer é empilhar um monte desses somadores juntos e alimentá-los com números, então aqui está um somador apenas de esteiras calculando 01001101 (77) + 10001011 (139) = 011011000 (216):
Somar números é legal e tudo, mas não é nada sem algum tipo de memória, que é exatamente o que exploraremos na próxima edição. Fique ligado!
Contribuindo
Como sempre, estamos procurando pessoas que queiram contribuir com o Alt-F4, seja enviando um artigo ou ajudando com a tradução. Se você tem algo interessante em mente que deseja compartilhar com a comunidade de uma forma refinada, este é o lugar para fazê-lo. Se você não tiver certeza sobre isso, teremos o prazer de ajudar discutindo ideias de conteúdo e questões estruturais. Se você se identifica com essa situação, junte-se ao nosso servidor no Discord para começar!