Alt-F4 #47 - 优化解决方案 2021-09-17
翻译 Ph.X

Alt-F4 经过三周的休整现已复工,而且比以往任何时候都更有动力! 复刊第一炮由 ilbJanissary 来为我们深入介绍 FactorioLab 背后的计算引擎是如何运转的。虽然看起来很复杂,但这个过程被分解成细小的部分,并辅以实例加以说明。阅读这篇文章时,不会有眼睛发花的情况(希望如此!)。
优化解决方案 ilbJanissary
嗨!作为 Angular 的开发者和柯克·麦克唐纳的计算器(KirkMcDonald’s Calculator)的长期用户,我在 2020 年决定为这个工厂游戏建立自己的计算器网站,名为 FactorioLab。Kirk McDonald 发布了一篇关于他所用方法的短文,帮助我入门,但并没有解释它用来求解的算法。在数学的汪洋中挣扎了一段时间,并在 FactorioLab 中建立了两个迭代的非单项式求解器后,我希望与社区分享我在实现真正的单项式算法求解器时学到的东西。太长不看版可以在文章的末尾找到。
为什么要用计算器?
让我们从头开始。在异星工厂、戴森球计划和Satisfactory等工厂游戏中,游戏目标是开采原始资源,使用这些资源按照配方制造物品,并使用这些物品来发现更高级的物品和配方。在这些游戏的初期,所涉及的配方和物品很简单,不需要大量的计划,但随着更多的物品和配方的解锁,生产链会变得非常复杂。像 FactorioLab 和柯克·麦克唐纳的计算器这样的工厂计算器旨在帮助计算以一定速度持续生产某物品时需要多少原始资源和加工设施。
概念
在工厂游戏中有两个重要的概念,对于理解计算背后的数学很重要:物品 和 配方。
- 物品 是工厂游戏中的产品和原料。有些物品只作为中间物存在,本身不能做任何事情,如大多数原始资源。有些物品在游戏中也能起到一定的作用,如燃料、传送带、熔炉、装配机、发电机、配电站等。
- 配方 是玩家在游戏中制造新的、更高级的物品的方法。有些物品的配方可以用手工制造,而另外一些配方只能由特定的工厂建筑,如装配机或熔炉来完成。配方通常需要一组特定的物品作为输入,需要一定的时间来执行,并产生一组特定的物品作为产品。配方通常图示为一个箭头左边的原料清单和制造时间,指向箭头右边的产品清单。
例如,在异星工厂中,一个基本物品是 铁矿。铁矿 是一种原始资源,意味着它是通过一个无需任何物品作为输入的配方生产的:

这个配方可以在 铁矿 资源上手工制造,也可以用采矿机来制造。铁矿 主要用作生产 铁板 的原料,铁板使用如下配方:

铁板 不能用手工制造,必须在熔炉中生产。配方也可以包括多个输入和输出,例如异星工厂中比较复杂的配方之一,高等原油分馏。

这个配方只能用  炼油厂 来制造。
炼油厂 来制造。
制造速度
配方的实际制造时间也受用于制造该配方的机器的制造速度影响。例如,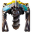 电力采矿机 的制造速度为
电力采矿机 的制造速度为 0.5,这意味着当它被用来使用上述配方开采 铁矿 时,每个 铁矿 实际耗时 2 秒。为了简化,我们一般将制造速度视为 1。
配方等式
你可能已经注意到,如果用等号代替箭头,可以很容易的将一个配方解释为一个等式。由于时间本身不是一个实际的物品,为了使这个等式有意义,我们需要将等式两边除以时间,从而将等式中的数字视为速率,而不是一个单纯的物品数量。因此,铁矿 配方变成了:

在这种情况下,等式左边是零,因为这个配方不需要任何输入。同样地,铁板 的配方变成了:
目前的这些方程求解相对简单。许多产品只能由一个配方生产,因此只需要简单的代数来确定以一定速度生产产品所涉及的物品和配方的数量。在 FactorioLab 中,如果所需的产品只能由一个配方生产,那么这些方程就会在生产链中尽可能地在上游求解。然而,有些产品可以通过多个不同的配方来生产,这就使得确定该用哪种配方变得更加复杂,包括每一种配方的数量,以优化降低原料需求。
配方矩阵
异星工厂中的典型问题是 高等原油分馏 和裂解,以下作为求解的主要样例。这个问题通常涉及至少五个配方和五种物品。这些配方是:
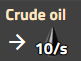
 原油(原料)
原油(原料)
原油的生产速度会根据地图上的资源而变化,但可以用简化的形式来处理。

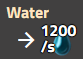
 水(原料)
水(原料)
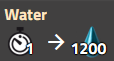
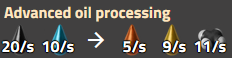
 高等原油分馏
高等原油分馏

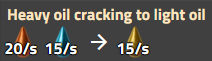
 重油裂解
重油裂解
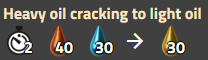
 轻油裂解
轻油裂解
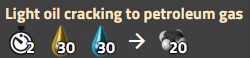
请注意,还可能涉及其他配方,如 基础原油分馏 和 煤炭液化,但这两个目前先忽略不计。
用这些配方除以它们的配方时间,可以得到一个基于速率的等式,这正是计算器计算生产需求所需的形式。由于所有涉及的工厂的制作速度都是 1,我们不需要做任何调整来考虑制作速度,但这对于许多工厂,或任何涉及插件或插件效果分享塔的时候都是必要的。
 原油(原料)
原油(原料)
 水(原料)
水(原料)
 高等原油分馏
高等原油分馏
 重油裂解
重油裂解
 轻油裂解
轻油裂解
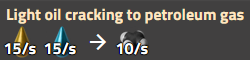
这些配方可以构成一个矩阵。这个矩阵的列表示配方,行表示物品。这就形成了一组不同的方程式,每个物品都有一个方程式。例如,对于原油有:10 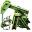 - 20
- 20  = # 输出
= # 输出 
将物品数量除以其配方数量后,完整的矩阵如下:
 |
 |
 |
 |
 |
|
|---|---|---|---|---|---|
 |
10 | 0 | -20 | 0 | 0 |
 |
0 | 1200 | -10 | -15 | -15 |
 |
0 | 0 | 5 | -20 | 0 |
 |
0 | 0 | 9 | 15 | -15 |
 |
0 | 0 | 11 | 0 | 10 |
接下来,我们需要说明实际想生产什么。为了处理这个问题,我们可以添加一列来表示我们工厂的最终产出。举个例子,假设我们想生产 5  重油/秒和 100
重油/秒和 100  石油气/秒。为了在矩阵中体现这个需求,我们设这些数值为负数,表示我们正在从系统中取出这个数量。
石油气/秒。为了在矩阵中体现这个需求,我们设这些数值为负数,表示我们正在从系统中取出这个数量。
 |
 |
 |
 |
 |
输出 | |
|---|---|---|---|---|---|---|
 |
10 | 0 | -20 | 0 | 0 | 0 |
 |
0 | 1200 | -10 | -15 | -15 | 0 |
 |
0 | 0 | 5 | -20 | 0 | -5 |
 |
0 | 0 | 9 | 15 | -15 | 0 |
 |
0 | 0 | 11 | 0 | 10 | -100 |
线性规划
这种性质的矩阵在数学上被称为线性规划,可以用线性规划技术来解决。求解线性规划最常见的方法是单纯形法,这也是 FactorioLab 和柯克·麦克唐纳的计算器所使用的方法。由于该线性规划有多个可能的解,单纯形法采取了最大化目标函数的方法,可视为矩阵的另一行。
虽然在线性规划中不一定有我们想要最大化的值,但我们确实希望最小化生产物品所需的资源和设施数量。因此,我们可以在线性规划中先添加一个“代价”函数,而非最大化的目标,来描述我们如何在解决方案中最小化资源和工厂的数量。
为什么我们需要一个代价函数?
对于每个工厂只有一个配方的简单厂区,我们甚至不需要代价函数。我们可以计算出我们需要多少种原料,然后继续沿着配方链往下走,直到我们得到一个解决方案。那么,为什么线性规划需要一个代价函数呢?
让我们来看看异星工厂中石油加工的例子。在我们的样例中,我们希望生产  石油气 和
石油气 和  重油。请注意
重油。请注意  高等原油分馏 同时生成两种产物。 因此,一个可行的解决方案是完全不考虑裂解配方,靠
高等原油分馏 同时生成两种产物。 因此,一个可行的解决方案是完全不考虑裂解配方,靠  高等原油分馏 直接生产我们所需的所有石油产品。那么,为什么我们还要在异星工厂中使用裂解呢?有两个主要原因:
高等原油分馏 直接生产我们所需的所有石油产品。那么,为什么我们还要在异星工厂中使用裂解呢?有两个主要原因:
- 这个等式是不平衡的,这意味着在几乎所有的工厂中,产出的油品与所需的油品比例不一致,最终其中一个产物将填满所有储罐,并迫使生产完全停止。在大多数生产纯科学产品的工厂中,罪魁祸首是
 轻油。异星工厂中没有办法直接“烧掉”多余的油,而且手动清空储油罐也很乏味。
轻油。异星工厂中没有办法直接“烧掉”多余的油,而且手动清空储油罐也很乏味。 - 它会消耗额外的
 原油。原油 不像水那样容易获取,所以我们通常希望尽量减少所需的数量。通过将多余的 轻油 裂解成 石油气,我们既可以解决多余的 轻油,又可以减少所需的 原油 量,代价是额外的
原油。原油 不像水那样容易获取,所以我们通常希望尽量减少所需的数量。通过将多余的 轻油 裂解成 石油气,我们既可以解决多余的 轻油,又可以减少所需的 原油 量,代价是额外的  水,而这很容易获取。
水,而这很容易获取。
代价函数量化了获得资源的难度,以及建立工厂所需的工作量。一个需要较少资源的解决方案比一个需要大量资源的解决方案更好,一个需要较少工厂的解决方案比一个需要更多工厂的解决方案好。通过把获得资源和建立工厂的代价表示为具体的数字上,我们可以量化一个解决方案的代价,而计算器可以使用这个代价来确定哪个解决方案是最佳的。
我们如何定义一个代价函数?
代价函数可以是相当抽象和随意的,因为在异星工厂和戴森球计划等游戏中没有具体的资源和工厂的成本。相反,我们必须依靠直觉来判断什么是最难获得和布置的工厂。在 FactorioLab 中,这归结为几个定义代价函数的具体变量。
- 一个执行单一配方的工厂代价是 1。
- 一单位的
 水 代价是 100,因为水相对易得。
水 代价是 100,因为水相对易得。 - 一单位的
 原油 代价是 1000,因为它的产量一般高于其他开采的资源。
原油 代价是 1000,因为它的产量一般高于其他开采的资源。 - 一单位的“开采”资源代价是 10,000。在异星工厂种这是指 煤矿,铀矿,石矿,铁矿 和 铜矿。一般来说,这是我们希望消耗最少的资源。
- 一单位的“手动采集”资源代价是 100,000。在运行过程中这是指 木材。虽然 木材 在原版异星工厂中通常不是任何重要配方的一部分,但我们希望尽量减少我们对任何无法自动收集资源的使用。
我们可以把这个成本函数表示为我们矩阵中的额外一行。为了准确说明开采资源的成本,我们将简化这些配方,使成本基于物品的数量,而不是开采资源的工厂数量。因此, 抽油机 和
抽油机 和  供水泵 的配方被简化为一个成本较高且每秒只生产 1 单位的配方。一旦我们计算出解决方案所需的
供水泵 的配方被简化为一个成本较高且每秒只生产 1 单位的配方。一旦我们计算出解决方案所需的  原油 和
原油 和  水 的数量,再将这个生产数量转换回所需工厂数量是很简单的。
水 的数量,再将这个生产数量转换回所需工厂数量是很简单的。
 |
 |
 |
 |
 |
输出 | |
|---|---|---|---|---|---|---|
 |
1 | 0 | -20 | 0 | 0 | 0 |
 |
0 | 1 | -10 | -15 | -15 | 0 |
 |
0 | 0 | 5 | -20 | 0 | -5 |
 |
0 | 0 | 9 | 15 | -15 | 0 |
 |
0 | 0 | 11 | 0 | 10 | -100 |
| 代价 | 1000 | 100 | 1 | 1 | 1 | 0 |
对偶最小化问题
现在,这个线性优化的问题是,我们想要最小化我们的解的成本,而单纯形法被设计为最大化一个目标。幸运的是,有一个简单的方法可以将最小化问题转换为最大化问题,从而可以用单纯形法来解决。这是通过将最小化问题转换为其“对偶最大化问题”来实现的。一旦最小化问题被转换为其对偶最大化问题,就能用单纯形法解决对偶问题。对偶问题最大化的解与原始问题最小化的解相同,所以我们可以接受这一解作为我们的最优解。
对偶问题只是原问题的转置,或交换行和列的位置。结果为:
 |
 |
 |
 |
 |
代价 | |
|---|---|---|---|---|---|---|
 |
1 | 0 | 0 | 0 | 0 | 1000 |
 |
0 | 1 | 0 | 0 | 0 | 100 |
 |
-20 | -10 | 5 | 9 | 11 | 1 |
 |
0 | -15 | -20 | 15 | 0 | 1 |
 |
0 | -15 | 0 | -15 | 10 | 1 |
| 输出 | 0 | 0 | -5 | 0 | -100 | 0 |
为了处理潜在的剩余价值,线性规划通常会在程序中加入“剩余”或“松弛”变量。例如,对于一个只生产  重油 的工厂来说,没有一个解不涉及一些剩余的
重油 的工厂来说,没有一个解不涉及一些剩余的  轻油 和
轻油 和  石油气。这些由矩阵中的附加列表示的,每一列都有一个’1’的值位于与该列物品所匹配的行中。
石油气。这些由矩阵中的附加列表示的,每一列都有一个’1’的值位于与该列物品所匹配的行中。
 |
 |
 |
 |
 |
+
|
+
|
+
|
+
|
+
|
代价 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
 |
1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1000 |
 |
0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 100 |
 |
-20 | -10 | 5 | 9 | 11 | 0 | 0 | 1 | 0 | 0 | 1 |
 |
0 | -15 | -20 | 15 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
 |
0 | -15 | 0 | -15 | 10 | 0 | 0 | 0 | 0 | 1 | 1 |
| 输出 | 0 | 0 | -5 | 0 | -100 | 0 | 0 | 0 | 0 | 0 | 0 |
现在,我们终于有了一个可以用单纯形法求解的规范矩阵。
用单纯形法求解
单纯形法的最终目标是得出一个矩阵,其中目标函数(在这种情况下,矩阵的最后一行)不包含负数。在我们的初始矩阵中,注意我们的目标行有两列负值,代表我们想要生产的两个项目。为了达到我们的解,我们只需要应用“转轴”操作,直到我们的目标行不再有任何负值。
转轴 1
A Simplex pivot operation involves four steps.
- 选择一列进行转轴。必须是一个包含负数的列,通常选绝对值最大的负数。在我们的矩阵中,这将是
 石油气 列。
石油气 列。 - 选择一行进行转轴。检查每一行,如果所选列的值大于 0,计算该行的代价列与该行所选列的值的比。转轴行是比值最低的那一行。在我们的矩阵中,我们可以检查每一行:
-
 :
:  列是 0,忽略此行。
列是 0,忽略此行。 -
 :
:  列是 0,忽略此行。
列是 0,忽略此行。 -
 :
:  列是 11,代价列是 1,所以比值为 1/11。
列是 11,代价列是 1,所以比值为 1/11。 -
 :
:  列是 0,忽略此行。
列是 0,忽略此行。 -
 :
:  列是 10,代价列是 1,所以比值为 1/10。
列是 10,代价列是 1,所以比值为 1/10。 - 比值最低的是
 行,为 1/11,所以我们选择这一行进行转轴。
行,为 1/11,所以我们选择这一行进行转轴。
-
- 用转轴行除以主元的倒数。在我们的转轴行中,结果为 -20/11,-10/11,5/11,9/11,1,0,0,1/11,0,0,1/11
- 将转轴行的倍数添加到其他行中,将转轴列改为 0。最后的结果是:
+
|
+
|
+
|
+
|
+
|
 |
 |
 |
 |
 |
代价 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1000 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 100 |
| -1 9/11 | -10/11 | 5/11 | 9/11 | 1 | 0 | 0 | 1/11 | 0 | 0 | 1/11 |
| 0 | -15 | -20 | 15 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 18 2/11 | -5 10/11 | -4 6/11 | -23 2/11 | 0 | 0 | 0 | -10/11 | 0 | 1 | 1/11 |
| -181 + 9/11 | -90 10/11 | 40 5/11 | 81 9/11 | 0 | 0 | 0 | 9 1/11 | 0 | 0 | 9 1/11 |
现在,让我们继续下一次转轴。
转轴 2
第 1 列(-181 9/11),第 5 行(比值 1/200)
+
|
+
|
+
|
+
|
+
|
 |
 |
 |
 |
 |
代价 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 13/40 | 1/4 | 1 + 11/40 | 0 | 1 | 0 | 1/20 | 0 | -11/200 | 9999 + 199/200 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 100 |
| 0 | -1 1/2 | 0 | -1 1/2 | 1 | 0 | 0 | 0 | 0 | 1/10 | 1/10 |
| 0 | -15 | -20 | 15 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 1 | -13/40 | -1/4 | -1 11/40 | 0 | 0 | 0 | -1/20 | 0 | 11/200 | 1/200 |
| 0 | -150 | -5 | -150 | 0 | 0 | 0 | 0 | 0 | 10 | 10 |
转轴 3
第 2 列(-150),第 2 行(比值 100)
+
|
+
|
+
|
+
|
+
|
 |
 |
 |
 |
 |
代价 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1/4 | 1 + 11/40 | 0 | 1 | -13/40 | 1/20 | 0 | -11/200 | 9967 + 99/200 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 100 |
| 0 | 0 | 0 | -1 1/2 | 1 | 0 | 1 1/2 | 0 | 0 | 1/10 | 150 + 1/10 |
| 0 | 0 | -20 | 15 | 0 | 0 | 15 | 0 | 1 | 0 | 1501 |
| 1 | 0 | -1/4 | -1 11/40 | 0 | 0 | 13/40 | -1/20 | 0 | 11/200 | 32 + 101/200 |
| 0 | 0 | -5 | -150 | 0 | 0 | 150 | 0 | 0 | 10 | 15010 |
转轴 4
第 4 列(-150),第 4 行(比值 133 2/5)
+
|
+
|
+
|
+
|
+
|
 |
 |
 |
 |
 |
代价 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 19/20 | 0 | 0 | 1 | -1 3/5 | 1/20 | -17/200 | -11/200 | 9839 91/100 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 100 |
| 0 | 0 | -2 | 0 | 1 | 0 | 3 | 0 | 1/10 | 1/10 | 300 + 1/5 |
| 0 | 0 | -1 1/3 | 1 | 0 | 0 | 1 | 0 | 1/15 | 0 | 100 1/15 |
| 1 | 0 | -1 19/20 | 0 | 0 | 0 | 1 3/5 | -1/20 | 17/200 | 11/200 | 160 9/100 |
| 0 | 0 | -205 | 0 | 0 | 0 | 300 | 0 | 10 | 10 | 30020 |
转轴 5
第 3 列(-205),第 1 行(比值 5046 7/65)
+
|
+
|
+
|
+
|
+
|
 |
 |
 |
 |
 |
代价 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 20/39 | -32/39 | 1/39 | -17/390 | -11/390 | 5046 7/65 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 100 |
| 0 | 0 | 0 | 0 | 1 | 1 1/39 | 1 14/39 | 2/39 | 1/78 | 17/390 | 10392 27/65 |
| 0 | 0 | 0 | 1 | 0 | 80/117 | -11/117 | 4/117 | 1/117 | -22/585 | 6828 41/195 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1000 |
| 0 | 0 | 0 | 0 | 0 | 105 5/39 | 131 31/39 | 5 10/39 | 1 5/78 | 4 17/78 | 1064472 1/13 |
矩阵的最后一行现在没有负值,所以这被认为是一个解。解决方案可以从最后一行中提取出来,前五列代表剩余值(在样例情况下,全部为零),接下来的两个值代表输入的  原油 和
原油 和  水,接下来的三个值代表运行
水,接下来的三个值代表运行  高等原油分馏 的工厂数,
高等原油分馏 的工厂数, 重油裂解 的工厂数和
重油裂解 的工厂数和  轻油裂解的工厂数,以及最好一个值代表这个解的“代价”。
轻油裂解的工厂数,以及最好一个值代表这个解的“代价”。
因此,我们的解决方案需要 105 5/39  ,131 31/39
,131 31/39  ,5 10/39
,5 10/39 
 ,1 5/78
,1 5/78 
 和 4 17/78
和 4 17/78 
 。
。
这个解可以与 FactorioLab 中的结果相对比。
矩阵标签页
FactorioLab 的 Matrix 标签页是一个相对较新的功能,它允许你窥探单纯形法求解器的内部情况。对于不使用单纯形法求解的配方链来说,这个标签页大多是空白的,但当使用单纯形法时,这个选项卡会暴露出许多细节,甚至允许你自定义求解器使用的代价函数。
结果信息
第一张表展示了当前单纯形法求解结果的细节。
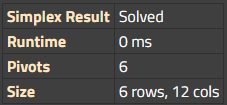
- 求解器的单纯形结果
- 跳过:单纯形求解器未被使用,要么是因为它被禁用,要么是因为解算配方链时不需要它。
- 失败:单纯形求解器遇到了错误,通常是由于配方循环无法解决(例如,如果铁板需要两个铁齿轮,铁齿轮需要两个铁板)。
- 取消:用户在运行了至少 5 秒钟后,在提示下手动取消了求解器。
- 有解:找到了一个有效的解。
- 单纯形求解器的 运行时间,单位毫秒
- 求解器总计执行的 转轴 次数
- 规范矩阵的 大小
代价修改器
第二个表格允许用户调整规范矩阵中使用的代价函数。
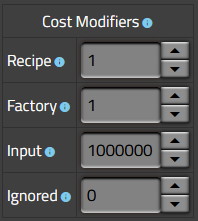
- 配方 是一个乘以具有确定成本的配方的成本的系数,通常是代表原材料的采矿配方
- 工厂 是一个乘以工厂本身数量的成本的系数,这通常只是一个次要因素。
- 输入 定义了不能由任何配方生产的物品的成本,例如异星工厂中的木材
- 忽略 定义了被明确忽略的物品的成本,默认为零。
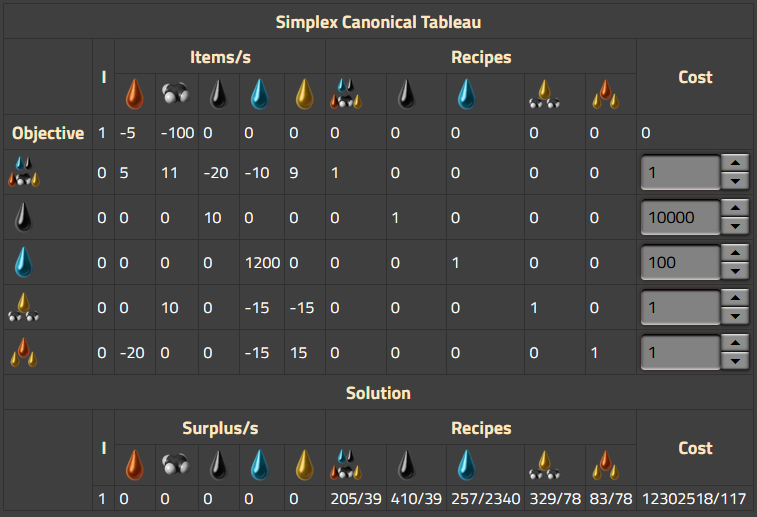
单纯形规范表和解决方案
第三张表显示了由计算器生成的规范矩阵和最终成本的解决方案行。请注意,这显示的是对偶最小化问题,这就是计算器使用单纯形法最小化成本的方式。在每个配方行中,显示的是该配方的成本,也可以用右边的成本输入字段进行覆盖。无论用户选择何种显示率,该表中的数值都表示为物品/秒,因为内部总是这样进行计算。
替代算法
事实证明,使用对偶最大化的单纯形法是一种解决工厂计算的高效的算法。然而,单纯形法并不是解决线性规划的唯一算法。还有其他一些方法例如修正单纯形法,纵横交叉算法, 椭球法, 卡马卡算法和内点法。事实上,就在 2019 年还通过高效矩阵乘法改进了计算用时。随着线性规划的增长,特别是在装 Mod 的异星工厂中,FactorioLab 使用的单纯形法可能需要很长的时间才能找到一个解,特别是当 Mod 引入“循环”配方时。进一步的研究有可能开发出一种更好的解决工厂线性规划的算法。
太长不看
- 当物品只由一个配方生产时,简单的工厂很容易手算出来。
- 当物品由多个不同的配方生产时,我们需要一种方法来计算出每个配方的用量。
- 由于有多个潜在的解决方案,我们需要衡量一个解决方案的 代价,以确定哪个是最好的。
- 单纯形法 是解决这类问题最常用的算法(尽管不是最快的),在异星工厂界和数学界都是如此。
-
FactorioLab 使用 单纯形法 算法来优化复杂工厂的解决方案,并允许用户:
- 定制 代价 函数,因为它是主观的
- 使用常见的 Mod 数据集
- 从移动设备或在工作时计算和规划工厂
- 计算你能从一个炼油厂生产多少火箭燃料
欢迎加入 FactorioLab Discord 来了解详情!
征稿
一如既往的,我们正在召集任何想要为 Alt-F4 做出贡献的人,无论是提交文章还是帮助翻译都可以。如果您有些有趣的想法,并乐于与社区分享,这里就是一个好地方。如果您没有太大把握,我们会很乐意帮助您讨论内容创意和结构问题。如果您有意参与,从加入 Discord 开始吧!